【深度学习】VAE变分自编码器原理推导+Python代码实现
1、前言变分自编码器是近些年较火的一个生成模型,我个人认为其本质上仍然是一个概率图模型,只是在此基础上引入了神经网络。本文将就变分自编码器(VAE)进行简单的原理讲解和数学推导。论文: Auto-Encoding Variational Bayes视频:2、引入2.1、高斯混合模型生成模型,可以简单的理解为生成数据(不止,但我们暂且就这么理解它)\boxed{(不止,但我们暂且就这么理解它)}(不
1、前言
变分自编码器是近些年较火的一个生成模型,我个人认为其本质上仍然是一个概率图模型,只是在此基础上引入了神经网络。本文将就变分自编码器(VAE)进行简单的原理讲解和数学推导。
论文: Auto-Encoding Variational Bayes
2、引入
2.1、高斯混合模型
生成模型,可以简单的理解为生成数据 ( 不止,但我们暂且就这么理解它 ) \boxed{(不止,但我们暂且就这么理解它)} (不止,但我们暂且就这么理解它)。假如现在我们有样本数据,而我们发现这些样本符合正态分布且样本具有充分的代表性,因此我们计算出样本的均值和方差,就能得到样本的概率分布。然后从正态分布中抽样,就能得到样本。 这种生成样本的过程就是生成过程 \boxed{\mathbf{这种生成样本的过程就是生成过程}} 这种生成样本的过程就是生成过程。
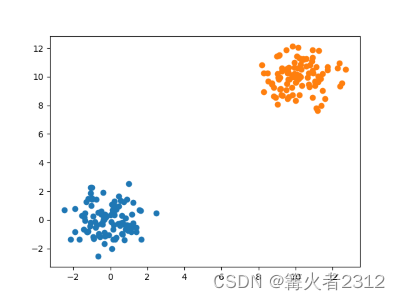
可是,假如我们的数据长这样

很显然,它的数据是由两个不同的正态分布构成。我们可以计算出这些样本的概率分布。但是一种更为常见的方法就是将其当作是两个正态分布。我们引入一个隐变量z。
假设 z 的取值为 0 , 1 \boxed{\mathbf{假设z的取值为0,1}} 假设z的取值为0,1,如果z为0,我们就从蓝色的概率分布中抽样;否则为1,则从橙色的概率分布中抽样。这就是生成过程。
但是这个隐变量z是什么?它其实就是隐藏特征 训练数据 x 的抽象出来的特征 \boxed{\mathbf{训练数据x的抽象出来的特征}} 训练数据x的抽象出来的特征,比如,如果x偏小,我们则认为它数据蓝色正太分布,否则为橙色。这个 “偏小” \boxed{“偏小”} “偏小”就是特征,我们把它的取值为0,1(0代表偏小,1代表偏大)。
那这种模型我们如何取训练它呢?如何去找出这个z呢? 一种很直观的方法就是重构代价最小 \boxed{\mathbf{一种很直观的方法就是重构代价最小}} 一种很直观的方法就是重构代价最小,我们希望,给一个训练数据x,由x去预测隐变量z,再由隐变量z预测回x,得到的误差最小。比如假如我们是蓝色正态分布,去提取特征z,得到的z再返回来预测x,结果得到的却是橙色的正态分布,这是不可取的。其模型图如下

这个模型被称为GMM高斯混合模型
2.2、变分自编码器(VAE)
那它和VAE有什么关联呢?其实VAE的模型图跟这个原理差不多。只是有些许改变, 隐变量 z 的维度是连续且高维的,不再是简单的离散分布 \boxed{\mathbf{隐变量z的维度是连续且高维的,不再是简单的离散分布}} 隐变量z的维度是连续且高维的,不再是简单的离散分布,因为假如我们生成的是图片,我们需要提取出来的特征明显是要很多的,传统的GMM无法做到。
在VAE中, q ( z ∣ x ) q(z|x) q(z∣x) (也就是用样本 x 预测变量 z ) \boxed{(也就是用样本x预测变量z)} (也就是用样本x预测变量z),其服从高斯分布,接下来,我们来看模型图

也就是将训练样本x给神经网络,让神经网络计算出均值和协方差矩阵 μ , log σ 2 \mu,\log \sigma^2 μ,logσ2 取 log 的原因是传统的神经网络输出值总是有正有负 \boxed{\mathbf{取\log的原因是传统的神经网络输出值总是有正有负}} 取log的原因是传统的神经网络输出值总是有正有负。有了这两个值就可以在对应的高斯分布中采样,得到隐变量z。再让z经过神经网络重构回样本,得到新样本。这就是整个VAE的大致过程了。
再次强调, 训练过程我们希望每次重构的时候,新样本和训练样本尽可能的相似 \boxed{\mathbf{训练过程我们希望每次重构的时候,新样本和训练样本尽可能的相似}} 训练过程我们希望每次重构的时候,新样本和训练样本尽可能的相似
如果我们这样直接去训练的化,可以吗?可以!但是会有个问题,神经网络会趋向于将协方差变0,而让概率分布 q ( z ∣ x ) q(z|x) q(z∣x)将不再具备随机性,概率分布空间会坍缩成一个点,每次采样都是均值,这种情况我们俗称过拟合。
为什么协方差会变成0?因为采样具有随机性,也就是存在噪声,噪声是肯定会增加重构的误差的。神经网络为了让误差最小,是肯定让这个随机性越小越好,因为只有这样,才能重构误差最小
但是我们肯定是希望有随机性的,为什么?因为有随机性,我们才可以生成不同的样本啊!
所以,对于概率分布 q ( z ∣ x ) q(z|x) q(z∣x),我们不希望它的协方差为0,所以我们需要对其进行约束。在论文中,它对其进行约束,要求它尽量的往 N ( 0 , I ) N(0,I) N(0,I)靠近( 其实与先验分布 P ( z ) 有关,后续数学推导中可见 , 假设 P ( z ) ∼ N ( z ∣ 0 , I ) \boxed{其实与先验分布P(z)有关,后续数学推导中可见,假设P(z)\sim N(z|0,I)} 其实与先验分布P(z)有关,后续数学推导中可见,假设P(z)∼N(z∣0,I))
所以,有KL散度去衡量两个概率分布的相似性
min
K
L
(
P
(
z
∣
x
)
∣
∣
P
(
z
)
)
\min KL\left(P(z|x)||P(z)\right)
minKL(P(z∣x)∣∣P(z))
KL散度是大于等于0的值,越小则证明越相似
K
L
(
q
(
x
)
∣
∣
p
(
x
)
)
=
∫
x
q
(
x
)
log
q
(
x
)
p
(
x
)
d
x
KL(q(x)||p(x))=\int_x q(x)\log\frac{q(x)}{p(x)}dx
KL(q(x)∣∣p(x))=∫xq(x)logp(x)q(x)dx
所以,我们就是两个优化目标
①最小化重构代价
②最小化上述的
K
L
散度
\boxed{\mathbf{①最小化重构代价}}\\ \boxed{\mathbf{②最小化上述的KL散度}}
①最小化重构代价②最小化上述的KL散度
依照这两个条件,建立目标函数,直接梯度下降
(
其实还需要重参数化,后面会讲到
)
\boxed{\mathbf{(其实还需要重参数化,后面会讲到)}}
(其实还需要重参数化,后面会讲到),刷刷刷地往下降,最终收敛。
下面,我们就对其进行简单的数学推导,并以此推导出目标函数
3、原理推导
3.1、引入目标函数
以VAE的简略图为例

设我们有N个样本
X
=
(
x
1
,
x
2
,
⋯
,
x
N
)
X=\begin{pmatrix}x^1,x^2,\cdots,x^N\end{pmatrix}
X=(x1,x2,⋯,xN)
定义隐变量先验分布
P
(
z
)
∼
N
(
0
,
I
)
P(z) \sim N(0,I)
P(z)∼N(0,I)。很自然的想法,我们直接对x求log极大似然,假设我们有N的样本,记作X。设所需求解的参数为
θ
\theta
θ,似然函数记为
P
θ
(
∣
x
)
P_\theta(|x)
Pθ(∣x),为了简便,以下省略
θ
\theta
θ,第
i
i
i个样本记为
x
i
x^{i}
xi,某个样本的第
j
j
j个维度记作
x
j
x_j
xj
log
P
(
X
)
=
log
P
(
x
1
)
P
(
x
2
)
⋯
P
(
x
N
)
=
log
∏
i
=
1
N
P
(
x
i
)
=
∑
i
=
1
N
log
P
(
x
i
)
\begin{aligned}\log P(X)=&\log P(x^1)P(x^2)\cdots P(x^N)\\=&\log\prod\limits_{i=1}^N P(x^i)\\=&\sum\limits_{i=1}^N\log P(x^i)\end{aligned}
logP(X)===logP(x1)P(x2)⋯P(xN)logi=1∏NP(xi)i=1∑NlogP(xi)
现在,我们先单独看看里面某一个样本的似然,某个样本记为
x
x
x
log
P
(
x
)
=
log
P
(
x
,
z
)
P
(
z
∣
x
)
=
log
P
(
x
,
z
)
−
log
P
(
z
∣
x
)
\begin{aligned}\log P(x)=&\log\frac{P(x,z)}{P(z|x)}\\=&\log P(x,z) -\log P(z|x)\end{aligned}
logP(x)==logP(z∣x)P(x,z)logP(x,z)−logP(z∣x)
引入一个
q
ϕ
(
z
∣
x
)
q_\phi(z|x)
qϕ(z∣x)分布,
ϕ
\phi
ϕ是它的参数,为了简便,后续省略掉
ϕ
\phi
ϕ,直接记为
q
(
z
∣
x
)
q(z|x)
q(z∣x)
log
P
(
x
)
\log P(x)
logP(x)等式左右分别对
q
(
z
∣
x
)
q(z|x)
q(z∣x)求积分
左边:
∫
z
log
P
(
x
)
q
(
z
∣
x
)
d
z
=
log
P
(
x
)
∫
z
q
(
z
∣
x
)
d
z
=
log
P
(
x
)
\begin{aligned}&\mathbf{左边:}\int_z \log P(x)q(z|x)dz=\log P(x)\int_z q(z|x)dz=\log P(x) \\\end{aligned}
左边:∫zlogP(x)q(z∣x)dz=logP(x)∫zq(z∣x)dz=logP(x)
所以左边等于右边
log
P
(
x
)
=
∫
z
(
log
P
(
x
,
z
)
−
log
P
(
z
∣
x
)
)
q
(
z
∣
x
)
d
z
=
∫
z
(
log
P
(
x
,
z
)
q
(
z
∣
x
)
−
log
P
(
z
∣
x
)
q
(
z
∣
x
)
)
q
(
z
∣
x
)
d
z
=
∫
z
log
P
(
x
,
z
)
q
(
z
∣
x
)
q
(
z
∣
x
)
d
z
−
∫
z
log
P
(
z
∣
x
)
q
(
z
∣
x
)
q
(
z
∣
x
)
d
z
=
∫
z
log
P
(
x
,
z
)
q
(
z
∣
x
)
q
(
z
∣
x
)
d
z
⏟
①
+
K
L
(
q
(
z
∣
x
)
∣
∣
P
(
z
∣
x
)
)
⏟
②
\begin{align}\log P(x)=&\int_z (\log P(x,z)-\log P(z|x))q(z|x)dz\tag{a}\\=&\int_z (\log \frac{P(x,z)}{q(z|x)}-\log \frac{P(z|x)}{q(z|x)})q(z|x)dz\tag{b}\\=&\int_{z}\log\frac{P(x,z)}{q(z|x)}q(z|x)dz-\int_z\log\frac{P(z|x)}{q(z|x)}q(z|x)dz\nonumber\\=&\underbrace{\int_{z}\log\frac{P(x,z)}{q(z|x)}q(z|x)dz}_{①}+\underbrace{KL(q(z|x)||P(z|x))}_{②}\nonumber\end{align}
logP(x)====∫z(logP(x,z)−logP(z∣x))q(z∣x)dz∫z(logq(z∣x)P(x,z)−logq(z∣x)P(z∣x))q(z∣x)dz∫zlogq(z∣x)P(x,z)q(z∣x)dz−∫zlogq(z∣x)P(z∣x)q(z∣x)dz①
∫zlogq(z∣x)P(x,z)q(z∣x)dz+②
KL(q(z∣x)∣∣P(z∣x))(a)(b)
(式a)到(式b)用到了
log
\log
log的性质。
那么,现在,我们开始极大似然,似然函数的参数为
θ
\theta
θ
max
θ
log
P
(
x
)
=
max
θ
(
∫
z
log
P
(
x
,
z
)
q
(
z
∣
x
)
q
(
z
∣
x
)
d
z
⏟
①
+
K
L
(
q
(
z
∣
x
)
∣
∣
P
(
z
∣
x
)
)
⏟
②
)
\max\limits_{\theta}\log P(x)=\max\limits_{\theta}\left(\underbrace{\int_{z}\log\frac{P(x,z)}{q(z|x)}q(z|x)dz}_{①}+\underbrace{KL(q(z|x)||P(z|x))}_{②}\right)
θmaxlogP(x)=θmax
①
∫zlogq(z∣x)P(x,z)q(z∣x)dz+②
KL(q(z∣x)∣∣P(z∣x))
因为
P
(
z
∣
x
)
P(z|x)
P(z∣x)我们算不出来(原因请看,分母的积分计算不了)
P
(
z
∣
x
)
=
P
(
z
,
x
)
P
(
x
)
=
P
(
x
∣
z
)
P
(
z
)
∫
P
(
x
∣
z
)
P
(
z
)
d
z
P(z|x)=\frac{P(z,x)}{P(x)}=\frac{P(x|z)P(z)}{\int P(x|z)P(z)dz}
P(z∣x)=P(x)P(z,x)=∫P(x∣z)P(z)dzP(x∣z)P(z)
故而,使用
q
(
z
∣
x
)
q(z|x)
q(z∣x)去逼近,所以,更新q的参数
ϕ
\phi
ϕ,以最小化第②项。
min
ϕ
K
L
(
q
(
z
∣
x
)
∣
∣
P
(
z
∣
x
)
)
\min\limits_{\phi} KL(q(z|x)||P(z|x))
ϕminKL(q(z∣x)∣∣P(z∣x))
在给定x跟
θ
\theta
θ的情况下,
log
P
(
x
)
\log P(x)
logP(x)的值是确定的,所以最小化第②项,就等于最大化第①项
max
ϕ
∫
z
log
P
(
x
,
z
)
q
(
z
∣
x
)
q
(
z
∣
x
)
d
z
↔
min
ϕ
K
L
(
q
(
z
∣
x
)
∣
∣
P
(
z
∣
x
)
)
\max\limits_{\phi} \int_{z}\log\frac{P(x,z)}{q(z|x)}q(z|x)dz \leftrightarrow\min\limits_{\phi} KL(q(z|x)||P(z|x))
ϕmax∫zlogq(z∣x)P(x,z)q(z∣x)dz↔ϕminKL(q(z∣x)∣∣P(z∣x))
举个例子,在VAE中,里面的参数
θ
,
ϕ
\theta,\phi
θ,ϕ,其实都是用神经网络去逼近的。所以,如果按照刚刚提到的,步骤就长这样
步骤①:固定
θ
参数,利用梯度下降
,
更新参数
ϕ
,
以最小化②
步骤②:固定
ϕ
参数,利用梯度下降
,
更新参数
θ
,
以最大化①
\mathbf{步骤①:固定\theta参数,利用梯度下降,更新参数\phi,以最小化②}\\\mathbf{步骤②:固定\phi参数,利用梯度下降,更新参数\theta,以最大化①}
步骤①:固定θ参数,利用梯度下降,更新参数ϕ,以最小化②步骤②:固定ϕ参数,利用梯度下降,更新参数θ,以最大化①
按照上面提到的,我们可以把第一步改成
步骤①:固定
θ
参数,利用梯度下降
,
更新参数
ϕ
,
以最大化①
\mathbf{步骤①:固定\theta参数,利用梯度下降,更新参数\phi,以最大化①}
步骤①:固定θ参数,利用梯度下降,更新参数ϕ,以最大化①
更一般地,我们把它们写成一起
max
θ
,
ϕ
∫
z
log
P
(
x
,
z
)
q
(
z
∣
x
)
q
(
z
∣
x
)
d
z
\max\limits_{\theta,\phi} \int_{z}\log\frac{P(x,z)}{q(z|x)}q(z|x)dz
θ,ϕmax∫zlogq(z∣x)P(x,z)q(z∣x)dz
由于KL散度是大于等于0的,所以第①项,就被称为变分下界。
log
P
(
x
)
≥
∫
z
log
P
(
x
,
z
)
q
(
z
∣
x
)
q
(
z
∣
x
)
d
z
\log P(x)\ge\int_{z}\log\frac{P(x,z)}{q(z|x)}q(z|x)dz
logP(x)≥∫zlogq(z∣x)P(x,z)q(z∣x)dz
好,现在我们只需要最大化其变分下界(以下省略掉参数)
max
∫
z
log
P
(
x
,
z
)
q
(
z
∣
x
)
q
(
z
∣
x
)
d
z
=
max
∫
z
log
P
(
x
∣
z
)
P
(
z
)
q
(
z
∣
x
)
q
(
z
∣
x
)
d
z
=
max
∫
z
(
log
P
(
z
)
q
(
z
∣
x
)
+
log
P
(
x
∣
z
)
)
q
(
z
∣
x
)
d
z
=
max
∫
z
log
P
(
x
∣
z
)
q
(
z
∣
x
)
d
z
−
∫
log
q
(
z
∣
x
)
P
(
z
)
q
(
z
∣
x
)
d
z
=
max
(
E
z
∼
q
(
z
∣
x
)
[
log
P
(
x
∣
z
)
]
⏟
①
−
K
L
(
q
(
z
∣
x
)
∣
∣
P
(
z
)
)
⏟
②
)
\begin{aligned}&\max \int_{z}\log\frac{P(x,z)}{q(z|x)}q(z|x)dz\\=&\max \int_z\log \frac{P(x|z)P(z)}{q(z|x)}q(z|x)dz\\=&\max \int_z \left(\log \frac{P(z)}{q(z|x)}+\log P(x|z)\right)q(z|x)dz\\=&\max \int_z\log P(x|z)q(z|x)dz-\int \log \frac{q(z|x)}{P(z)}q(z|x)dz\\=&\max \left(\underbrace{\mathbb{E}_{z\sim q(z|x)}\left[\log P(x|z)\right]}_{①} -\underbrace{KL(q(z|x)||P(z))}_{②}\right)\end{aligned}
====max∫zlogq(z∣x)P(x,z)q(z∣x)dzmax∫zlogq(z∣x)P(x∣z)P(z)q(z∣x)dzmax∫z(logq(z∣x)P(z)+logP(x∣z))q(z∣x)dzmax∫zlogP(x∣z)q(z∣x)dz−∫logP(z)q(z∣x)q(z∣x)dzmax(①
Ez∼q(z∣x)[logP(x∣z)]−②
KL(q(z∣x)∣∣P(z)))
发现了吗,最大化里面的第一项就期望,不就是从 q ( z ∣ x ) q(z|x) q(z∣x)采样z,再让 log P ( x ∣ z ) \log P(x|z) logP(x∣z)概率最大。这不就是重构代价最小吗;而对于第二项,最大化 − K L -KL −KL散度,就相当于最小化 K L KL KL散度。这和我们上面提到的两个优化目标是一样的。
3.2、细化目标函数
既然得到了目标函数,那么我们就对 log P ( x ∣ z ) \log P(x|z) logP(x∣z)似然和KL散度都求出具体的表达。
先来看 K L 散度 \boxed{先来看KL散度} 先来看KL散度
q
(
z
j
∣
x
)
∼
N
(
μ
ϕ
,
σ
ϕ
2
)
P
(
z
j
)
∼
N
(
0
,
1
)
q(z_j|x)\sim N(\mu_\phi,\sigma_\phi^2)\\P(z_j)\sim N(0,1)
q(zj∣x)∼N(μϕ,σϕ2)P(zj)∼N(0,1)
q
(
z
∣
x
)
q(z|x)
q(z∣x)需要逼近
P
(
z
)
P(z)
P(z),而
P
(
z
)
∼
N
(
0
,
I
)
P(z) \sim N(0,I)
P(z)∼N(0,I)的多维高斯分布,并且各个维度之间相互独立,所以
q
(
z
∣
x
)
q(z|x)
q(z∣x)也是如此设定,
那么最小化其KL散度,只需要对每一个维度求KL最小即可,单独看某一个维度,设某一个维度为
z
j
z_j
zj,设
q
(
z
j
∣
x
)
∼
N
(
μ
ϕ
,
σ
ϕ
2
)
q(z_j|x)\sim N(\mu_{\phi},\sigma^2_\phi)
q(zj∣x)∼N(μϕ,σϕ2)(后续为了简便,也同样将
ϕ
\phi
ϕ隐去)
min
K
L
(
q
(
z
j
∣
x
)
∣
∣
P
(
z
j
)
)
=
min
∫
q
(
z
j
∣
x
)
log
q
(
z
j
∣
x
)
P
(
z
j
)
d
z
j
=
min
∫
q
(
z
j
∣
x
)
log
N
(
μ
,
σ
2
)
N
(
0
,
1
)
d
z
j
=
min
∫
q
(
z
j
∣
x
)
log
1
2
π
σ
exp
{
−
(
z
j
−
μ
)
2
2
σ
2
}
1
2
π
exp
{
−
z
j
2
2
}
d
z
j
=
min
∫
q
(
z
j
∣
x
)
log
1
σ
exp
{
−
(
z
j
−
μ
)
2
2
σ
2
}
exp
{
−
z
j
2
2
}
d
z
j
=
min
∫
q
(
z
j
∣
x
)
(
log
1
σ
+
log
exp
{
−
(
z
j
−
μ
)
2
2
σ
2
}
exp
{
−
z
j
2
2
}
)
d
z
j
=
min
∫
q
(
z
j
∣
x
)
(
log
1
σ
+
log
exp
{
−
(
z
j
−
μ
)
2
2
σ
2
+
z
j
2
2
}
)
d
z
j
=
min
∫
q
(
z
j
∣
x
)
(
log
1
σ
−
(
z
j
−
μ
)
2
2
σ
2
+
z
j
2
2
)
d
z
j
=
min
∫
q
(
z
j
∣
x
)
1
2
(
2
log
1
σ
−
(
z
j
−
μ
)
2
σ
2
+
z
j
2
)
d
z
j
=
min
1
2
∫
q
(
z
j
∣
x
)
(
z
j
2
−
log
σ
2
−
(
z
j
−
μ
)
2
σ
2
)
d
z
j
\begin{aligned}&\min KL(q(z_j|x)||P(z_j))\\=&\min \int q(z_j|x) \log\frac{q(z_j|x)}{P(z_j)}dz_j\\=&\min \int q(z_j|x)\log \frac{N(\mu,\sigma^2)}{N(0,1)}dz_j\\=&\min \int q(z_j|x) \log \frac{\frac{1}{\sqrt{2\pi}\sigma}\exp\{-\frac{(z_j-\mu)^2}{2\sigma^2}\}}{\frac{1}{\sqrt{2\pi}}\exp \{-\frac{z_j^2}{2}\}}dz_j\\=&\min \int q(z_j|x) \log \frac{\frac{1}{\sigma}\exp\{-\frac{(z_j-\mu)^2}{2\sigma^2}\}}{\exp \{-\frac{z_j^2}{2}\}}dz_j\\=&\min \int q(z_j|x) \left(\log \frac{1}{\sigma}+\log\frac{\exp\{-\frac{(z_j-\mu)^2}{2\sigma^2}\}}{\exp \{-\frac{z_j^2}{2}\}}\right)dz_j\\=&\min \int q(z_j|x) \left(\log \frac{1}{\sigma}+\log\exp\{-\frac{(z_j-\mu)^2}{2\sigma^2}+\frac{z_j^2}{2}\}\right)dz_j\\=&\min \int q(z_j|x) \left(\log \frac{1}{\sigma}-\frac{(z_j-\mu)^2}{2\sigma^2}+\frac{z_j^2}{2}\right)dz_j\\=&\min \int q(z_j|x) \frac{1}{2}\left(2\log \frac{1}{\sigma}-\frac{(z_j-\mu)^2}{\sigma^2}+z_j^2\right)dz_j\\=&\min \frac{1}{2}\int q(z_j|x)\left(z_j^2-\log \sigma^2-\frac{(z_j-\mu)^2}{\sigma^2}\right)dz_j\end{aligned}
=========minKL(q(zj∣x)∣∣P(zj))min∫q(zj∣x)logP(zj)q(zj∣x)dzjmin∫q(zj∣x)logN(0,1)N(μ,σ2)dzjmin∫q(zj∣x)log2π1exp{−2zj2}2πσ1exp{−2σ2(zj−μ)2}dzjmin∫q(zj∣x)logexp{−2zj2}σ1exp{−2σ2(zj−μ)2}dzjmin∫q(zj∣x)
logσ1+logexp{−2zj2}exp{−2σ2(zj−μ)2}
dzjmin∫q(zj∣x)(logσ1+logexp{−2σ2(zj−μ)2+2zj2})dzjmin∫q(zj∣x)(logσ1−2σ2(zj−μ)2+2zj2)dzjmin∫q(zj∣x)21(2logσ1−σ2(zj−μ)2+zj2)dzjmin21∫q(zj∣x)(zj2−logσ2−σ2(zj−μ)2)dzj
可以分为三部分
min
K
L
(
q
(
z
j
∣
x
)
∣
∣
P
(
z
j
)
)
=
min
1
2
(
∫
q
(
z
j
∣
x
)
z
j
2
d
z
j
−
∫
q
(
z
j
∣
x
)
log
σ
2
d
z
j
−
∫
z
q
(
z
j
∣
x
)
(
z
j
−
μ
)
2
σ
2
d
z
j
)
\min KL(q(z_j|x)||P(z_j))=\min\frac{1}{2}\left( \int q(z_j|x)z_j^2 dz_j -\int q(z_j|x)\log \sigma^2 dz_j-\int_z q(z_j|x)\frac{(z_j-\mu)^2}{\sigma^2}dz_j\right)
minKL(q(zj∣x)∣∣P(zj))=min21(∫q(zj∣x)zj2dzj−∫q(zj∣x)logσ2dzj−∫zq(zj∣x)σ2(zj−μ)2dzj)
①:
∫
z
q
(
z
j
∣
x
)
z
j
2
d
z
=
E
[
z
j
2
]
=
D
(
z
j
)
+
E
[
z
j
]
2
=
σ
2
+
μ
2
②:
∫
z
q
(
z
j
∣
x
)
log
σ
2
d
z
j
=
log
σ
2
∫
z
q
(
z
j
∣
x
)
d
z
j
=
log
σ
2
③:
∫
z
q
(
z
j
∣
x
)
(
z
j
μ
)
2
σ
2
d
z
j
=
1
σ
2
∫
z
q
(
z
j
∣
x
)
(
z
j
μ
)
2
d
z
j
=
1
σ
2
E
[
(
z
j
−
μ
)
2
]
=
1
\begin{align}①:&\int_z q(z_j|x)z_j^2 dz=\mathbb{E}[z_j^2]=D(z_j)+\mathbb{E}[z_j]^2=\sigma^2+\mu^2\tag{A}\\②:&\int_z q(z_j|x)\log \sigma^2dz_j=\log\sigma^2\int_zq(z_j|x)dz_j=\log \sigma^2\tag{B} \\③:&\int_zq(z_j|x)\frac{(z_j\mu)^2}{\sigma^2}dz_j=\frac{1}{\sigma^2}\int_z q(z_j|x)(z_j\mu)^2dz_j=\frac{1}{\sigma^2}\mathbb{E}[(z_j-\mu)^2]=1\tag{C}\end{align}
①:②:③:∫zq(zj∣x)zj2dz=E[zj2]=D(zj)+E[zj]2=σ2+μ2∫zq(zj∣x)logσ2dzj=logσ2∫zq(zj∣x)dzj=logσ2∫zq(zj∣x)σ2(zjμ)2dzj=σ21∫zq(zj∣x)(zjμ)2dzj=σ21E[(zj−μ)2]=1(A)(B)(C)
对于(式
A
),里面用到了方差的计算公式
D
(
z
)
=
E
(
z
2
)
−
E
(
z
)
2
\boxed{\mathbf{对于(式A),里面用到了方差的计算公式D(z)=E(z^2)-E(z)^2}}
对于(式A),里面用到了方差的计算公式D(z)=E(z2)−E(z)2
对于(式 B ) , 是因为 q ( x j ∣ x ) 积分为 1 \boxed{\mathbf{对于(式B),是因为q(x_j|x)积分为1}} 对于(式B),是因为q(xj∣x)积分为1
对于(式
C
)
\boxed{\mathbf{对于(式C)}}
对于(式C)
1
σ
2
E
[
(
z
j
−
μ
)
2
]
=
1
σ
2
E
[
z
j
2
−
2
μ
z
j
+
μ
2
]
=
1
σ
2
(
E
(
z
j
2
)
−
2
μ
E
(
z
j
)
+
μ
2
)
=
1
σ
2
(
σ
2
+
μ
2
−
2
μ
2
+
μ
2
)
=
1
\begin{aligned}&\frac{1}{\sigma^2}\mathbb{E}[(z_j-\mu)^2]\\\\=&\frac{1}{\sigma^2}\mathbb{E}[z_j^2-2\mu z_j +\mu^2]\\=&\frac{1}{\sigma^2}\left(\mathbb{E}(z_j^2)-2\mu\mathbb{E}(z_j)+\mu^2\right)\\=&\frac{1}{\sigma^2}\left(\sigma^2+\mu^2-2\mu^2+\mu^2\right)\\=&1\end{aligned}
====σ21E[(zj−μ)2]σ21E[zj2−2μzj+μ2]σ21(E(zj2)−2μE(zj)+μ2)σ21(σ2+μ2−2μ2+μ2)1
如果你熟悉高斯分布的高阶矩的话,式A和式C完全就是二阶原点矩和中心距,是直接可以的得出答案的。
所以对于所有维度的
K
L
散度
,
有
(
假设隐变量有
J
维
)
\boxed{\mathbf{所以对于所有维度的KL散度,有(假设隐变量有J维)}}
所以对于所有维度的KL散度,有(假设隐变量有J维)
min
1
2
∑
j
=
1
J
(
σ
j
2
+
μ
j
2
−
log
σ
j
2
−
1
)
\min \frac{1}{2}\sum\limits_{j=1}^J(\sigma^2_j+\mu^2_j-\log \sigma^2_j -1 )
min21j=1∑J(σj2+μj2−logσj2−1)
再来看 log P ( x ∣ z ) 极大似然,即 max E q ( z ∣ x ) [ log P ( x ∣ z ) ] \boxed{\mathbf{再来看\log P(x|z)极大似然,即\max \mathbb{E}_{q(z|x)}[\log P(x|z)]}} 再来看logP(x∣z)极大似然,即maxEq(z∣x)[logP(x∣z)]。
值得注意的是,我看很多文章中都说此处就直接采用均方差来计算。这种说法是不准确的,在论文中提到 P ( x ∣ z ) P(x|z) P(x∣z)是服从一个概率分布的,而不是无端的就计算其差值。它不像是GAN一样,对于其隐藏在内部的概率分布不作约束,VAE是仍然对 P ( x ∣ z ) P(x|z) P(x∣z)进行约束。

“ log p θ ( x ( i ) ∣ z ( i , l ) ) 是伯努利或高斯 M L P ,这取决于我们建模的数据类型” \boxed{“\log p_θ (x^{(i)} |z^{(i,l)} )是伯努利或高斯MLP,这取决于我们建模的数据类型”} “logpθ(x(i)∣z(i,l))是伯努利或高斯MLP,这取决于我们建模的数据类型”
当然了,其实我们也可以不对其概率分布进行约束,归根究底,其让然是最小重构代价,那么我们的目标函数如果可以充分表达出“最小重构代价”,那么是什么又有何关系呢?
在论文中,其假设 P ( x ∣ z ) ∼ N ( μ , σ 2 I ) P(x|z) \sim N(\mu,\sigma^2 I) P(x∣z)∼N(μ,σ2I),其中 μ \mu μ和 σ 2 \sigma^2 σ2都是需要使用神经网络去逼近。
但是,一般地,我们假设 P ( x ∣ z ) ∼ ( f ( z ) , c I ) P(x|z) \sim (f(z),cI) P(x∣z)∼(f(z),cI),也就是其均值用神经网络去逼近,对于其协方差矩阵,我们设定为常数c和 I I I相乘,所以依然是各个维度之间相互独立。我们来看看它的极大似然估计得什么(假设采样n个样本)
max
E
q
(
z
∣
x
)
[
log
P
(
x
∣
z
)
]
≈
max
1
n
∑
i
=
1
n
log
P
(
x
∣
z
i
)
=
max
1
n
∑
i
=
1
n
log
1
2
π
D
/
2
∣
c
I
∣
1
/
2
exp
{
−
1
2
(
x
−
f
(
z
i
)
)
T
(
c
I
)
−
1
(
x
−
f
(
z
i
)
)
}
=
max
1
n
∑
i
=
1
n
log
1
2
π
D
/
2
∣
c
I
∣
1
/
2
−
1
2
(
x
−
f
(
z
i
)
)
T
(
c
I
)
−
1
(
x
−
f
(
z
i
)
)
∝
min
1
n
∑
i
=
1
n
(
x
−
f
(
z
i
)
)
T
(
x
−
f
(
z
i
)
)
=
min
1
n
∑
i
=
1
n
∣
∣
x
−
f
(
z
i
)
∣
∣
2
\begin{aligned}\max \mathbb{E}_{q(z|x)}[\log P(x|z)]\approx&\max\frac{1}{n}\sum\limits_{i=1}^n\log P(x|z^i)\\=&\max\frac{1}{n}\sum\limits_{i=1}^n\log \frac{1}{{2\pi }^{D/2}|cI|^{1/2}}\exp\left\{-\frac{1}{2}(x-f(z^i))^T(cI)^{-1}(x-f(z^i))\right\}\\=&\max\frac{1}{n}\sum\limits_{i=1}^n\log \frac{1}{{2\pi }^{D/2}|cI|^{1/2}}-\frac{1}{2}(x-f(z^i))^T(cI)^{-1}(x-f(z^i))\\\propto &\min \frac{1}{n}\sum\limits_{i=1}^n(x-f(z^i))^T(x-f(z^i))\\=&\min \frac{1}{n}\sum\limits_{i=1}^n||x-f(z^i)||^2\end{aligned}
maxEq(z∣x)[logP(x∣z)]≈==∝=maxn1i=1∑nlogP(x∣zi)maxn1i=1∑nlog2πD/2∣cI∣1/21exp{−21(x−f(zi))T(cI)−1(x−f(zi))}maxn1i=1∑nlog2πD/2∣cI∣1/21−21(x−f(zi))T(cI)−1(x−f(zi))minn1i=1∑n(x−f(zi))T(x−f(zi))minn1i=1∑n∣∣x−f(zi)∣∣2
可以看到,这就是一个均方差
综合得到最终目标函数表达式
\boxed{\mathbf{综合得到最终目标函数表达式}}
综合得到最终目标函数表达式
min
(
1
2
∑
j
=
1
J
(
σ
j
2
+
μ
j
2
−
log
σ
j
2
−
1
)
+
1
n
∑
i
=
1
n
∣
∣
x
−
f
(
z
i
)
∣
∣
2
)
\min \left(\frac{1}{2}\sum\limits_{j=1}^J(\sigma^2_j+\mu^2_j-\log \sigma^2_j -1 )+\frac{1}{n}\sum\limits_{i=1}^n||x-f(z^i)||^2\right)
min(21j=1∑J(σj2+μj2−logσj2−1)+n1i=1∑n∣∣x−f(zi)∣∣2)
3.3、重参数化技巧
有了目标函数,理论上我们直接梯度下降就可以了。然而,别忘了,我们是从 q ( z ∣ x ) q(z|x) q(z∣x)中采样出z来。可是我们却是用的神经网络去计算的均值和方差,得到的高斯分布再去采样,这种情况是不可导的。中间都已经出现了一个断层了。神经网络是一层套一层的计算。而采样计算了一层之后,从这一层中去采样新的值,再计算下一层。因此,采样本身是不可导的。
所以要引入重参数化技巧,假定
q
(
z
∣
x
)
∼
N
(
μ
,
σ
2
)
q(z|x) \sim N(\mu,\sigma^2)
q(z∣x)∼N(μ,σ2)。那么可以构造一个概率分布
p
(
ϵ
)
∼
N
(
0
,
1
)
p(\epsilon) \sim N(0,1)
p(ϵ)∼N(0,1)。有
z
=
μ
+
ϵ
σ
z=\mu +\epsilon\sigma
z=μ+ϵσ
我们从
P
(
ϵ
)
P(\epsilon)
P(ϵ)采样,然后利用上述公式,就相当于得到了从
q
(
z
∣
x
)
q(z|x)
q(z∣x)采样的采样值。
证明
\boxed{\mathbf{证明}}
证明
E
(
z
)
=
E
(
μ
)
+
E
(
ϵ
)
σ
=
μ
V
a
r
(
z
)
=
E
[
(
z
−
μ
)
2
]
=
E
[
(
ϵ
σ
)
2
]
=
σ
2
\begin{aligned}\mathbb{E}(z)=&\mathbb{E}(\mu)+\mathbb{E}(\epsilon)\sigma=\mu\\Var(z)=&\mathbb{E}[(z-\mu)^2]=\mathbb{E}[(\epsilon\sigma)^2]=\sigma^2\end{aligned}
E(z)=Var(z)=E(μ)+E(ϵ)σ=μE[(z−μ)2]=E[(ϵσ)2]=σ2
4、代码实现

效果一般,不晓得论文里面用了什么手段,效果看起来比这个好。(这个结果甚至还是我加了一层隐藏层的)
import torch
from torch.utils.data import DataLoader
from torchvision.datasets import MNIST
from torchvision.transforms import transforms
from torch import nn
from tqdm import tqdm
import matplotlib.pyplot as plt
class VAE(nn.Module):
def __init__(self,input_dim,hidden_dim,gaussian_dim):
super().__init__()
#编码器
#隐藏层
self.fc1=nn.Sequential(
nn.Linear(in_features=input_dim,out_features=hidden_dim),
nn.Tanh(),
nn.Linear(in_features=hidden_dim, out_features=256),
nn.Tanh(),
)
#μ和logσ^2
self.mu=nn.Linear(in_features=256,out_features=gaussian_dim)
self.log_sigma=nn.Linear(in_features=256,out_features=gaussian_dim)
#解码(重构)
self.fc2=nn.Sequential(
nn.Linear(in_features=gaussian_dim,out_features=256),
nn.Tanh(),
nn.Linear(in_features=256, out_features=512),
nn.Tanh(),
nn.Linear(in_features=512,out_features=input_dim),
nn.Sigmoid() #图片被转为为0,1的值了,故用此函数
)
def forward(self,x):
#隐藏层
h=self.fc1(x)
#计算期望和log方差
mu=self.mu(h)
log_sigma=self.log_sigma(h)
#重参数化
h_sample=self.reparameterization(mu,log_sigma)
#重构
reconsitution=self.fc2(h_sample)
return reconsitution,mu,log_sigma
def reparameterization(self,mu,log_sigma):
#重参数化
sigma=torch.exp(log_sigma*0.5) #计算σ
e=torch.randn_like(input=sigma,device=device)
result=mu+e*sigma #依据重参数化技巧可得
return result
def predict(self,new_x): #预测
reconsitution=self.fc2(new_x)
return reconsitution
def train():
transformer = transforms.Compose([
transforms.ToTensor(),
]) #归一化
data = MNIST("./data", transform=transformer,download=True) #载入数据
dataloader = DataLoader(data, batch_size=128, shuffle=True) #写入加载器
model = VAE(784, 512, 20).to(device) #初始化模型
optimer = torch.optim.Adam(model.parameters(), lr=1e-3) #初始化优化器
loss_fn = nn.MSELoss(reduction="sum") #均方差损失
epochs = 100 #训练100轮
for epoch in torch.arange(epochs):
all_loss = 0
dataloader_len = len(dataloader.dataset)
for data in tqdm(dataloader, desc="第{}轮梯度下降".format(epoch)):
sample, label = data
sample = sample.to(device)
sample = sample.reshape(-1, 784) #重塑
result, mu, log_sigma = model(sample) #预测
loss_likelihood = loss_fn(sample, result) #计算似然损失
#计算KL损失
loss_KL = torch.pow(mu, 2) + torch.exp(log_sigma) - log_sigma - 1
#总损失
loss = loss_likelihood + 0.5 * torch.sum(loss_KL)
#梯度归0并反向传播和更新
optimer.zero_grad()
loss.backward()
optimer.step()
with torch.no_grad():
all_loss += loss.item()
print("函数损失为:{}".format(all_loss / dataloader_len))
torch.save(model, "./model/VAE.pth")
if __name__ == '__main__':
#是否有闲置GPU
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
#训练
train()
#载入模型,预测
model=torch.load("./model/VAE (1).pth",map_location="cpu")
#预测20个样本
x=torch.randn(size=(20,20))
result=model.predict(x).detach().numpy()
result=result.reshape(-1,28,28)
#绘图
for i in range(20):
plt.subplot(4,5,i+1)
plt.imshow(result[i])
plt.gray()
plt.show()
5、结束
以上,就是VAE的原理和推导过程了。能力有限,过程并不严谨,如有问题,还望指出。阿里嘎多

更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容








所有评论(0)