扩散模型(Diffusion Model)

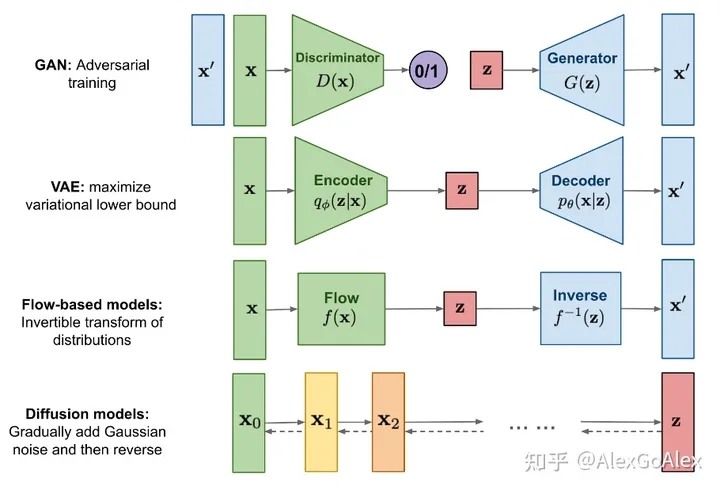
当前主要有四大生成模型：生成对抗模型、变分自动编码器、流模型以及扩散模型。
扩散模型（diffusion models）是当前深度生成模型中新SOTA。扩散模型在图片生成任务中超越了原SOTA：GAN，并且在诸多应用领域都有出色的表现，如计算机视觉，NLP、波形信号处理、多模态建模、分子图建模、时间序列建模、对抗性净化等。此外，扩散模型与其他研究领域有着密切的联系，如稳健学习、表示学习、强化学习。

下面学习李宏毅扩散模型课程的学习笔记。

简介

首先，先简单介绍一下Diffusion model，该模型有很多不同的变形，但以下的内容主要来自最知名的：
《Denosing Diffusion Probabilistic Models(DDPM)》

基本原理

Diffusion Model是如何运作的，怎么生成一张图片的？
首先，你要从高斯分布里采样出一张和目标图片大小一样的“图片”，比如256*256，这个“图片”全是杂讯，然后输入Denoise网络，输出的图片的杂讯就稍微滤掉一点。然后再输入Denoise…重复该过程，直到出现目标图片。
输入Denoise的次数是事先定好的。通常会给Denoise一个次数编号，如下图中，编号由大（模糊杂讯）到小（清晰图片）。1000步。
这些从杂讯到图片的步骤就叫作 Reverse Process。

在概念上，有点类似米开朗基洛说的：“雕像其实已经在大理石里面，我们不过是把不要的部分给去掉。”DIffusion Model就是假设图片信息本在杂讯里，我们不过是把不需要的杂讯给去掉。

每次Denoise Model其实是同一个模型，反复在用。但是，因为每个Denoise Model输入的图片相比，状况差异非常大，所以如果是同一个模型，会不会表现不是很好呢？我们给Denoise Model不仅输入图片，同时输入一个数字（代表现在图片杂讯严重程度，），如下图，直接输入第几个Step的信息。这样就可以反复用同一个模型。

Denoise Model内部实际做了什么事情呢？即它的具体结构
首先，里面有个Noise predictor噪声预测器，输入是杂讯图片x和一个数字（噪声程度），输出一张图片y，最终的输出是y减去x后的图片。

那可能有人问了，为什么要这么麻烦呢，为什么不是直接输入一张杂讯图片，输出Denoise的结果，直接训个端到端模型不行吗？
其实也可以，有人也确实这么做过，不过多数论文还是选择训一个噪声预测器。你想想，生成一张杂讯和生成一张猫的图片的难度是不一样的，可能learn一个噪声预测器是比较简单的，而learn一个端到端的模型是比较困难的。

那如何训练训一个噪声预测器Noise Predictor呢？
Denoise Model的任务我们已经知道了，那里面的Noise predictor要怎么训呢。
我们训练一个网络的时候就得有成对的数据才能训练呀，你要训Noise predictor输出一张杂讯图，就得有个ground truth呀，是不？

其实Noise predictor的训练资料是我们人为创造出来的。自给自足了。就是从database先拿出一张图片出来，人为给它加上噪声，产生有点噪声的图片，再加一些噪声上去，产生包含更多噪声的图片…以此类推， 最后整张图片全被噪声模糊了。然后把database里所有图片都这么加一遍噪。这个加噪声的过程，就叫做Forward Process，或者Diffusion process，前向处理。

做完前向处理的过程，我们就有Noise predictor的训练资料了。
对Noise predictor来说，输入就是如下蓝色框框的两部分，那么输出就是预测的噪声，即红色框的部分。

Text-to-Image任务

但是我们不止需要图片，在Text-to-Image任务中，需要把文字引入进来。

回忆一下之前做这个任务时，我们也需要大量成对的资料（文字-图片），ImageNet用100万张图训的，LAION用58.5亿张图片训的，难怪现在的模型能产生非常好的效果。
你可以去搜一下LAION里的图片，里面真的是啥都有，比如猫的图片，不仅有中文对应，还有日文和英文。

那这个任务中的Denoise是怎么做的？
非常简单，把文字加入进去就行。

那Denoise Model中的Noise predictor要怎么放呢？

和上面一样，对Noise predictor来说，输入就是如下蓝色框框的部分，之前是两部分，现在又多了一部分文字，即3个input，输出就是预测的噪声，即红色框的部分。

Denoising Diffusion Probabilitistic Models:

原始论文中的算法：

Stable Diffusion

今天比较好的图像生成模型，即使不是stable diffusion模型，它的套路也和stable diffusion差不多。今天就是介绍它后面的套路是什么。

一般里面都有三个组件，如下图。
1.Text encoder：把一段文字编码成一组向量
2.Generation Model：输入杂讯和文字的向量，输出一个“中间产物”（就是图片被压缩后的样子，可能人能看清，可能看不清）
3.Decoder：输入“中间产物”，输出图片
通常，这三个组件要分开训练，然后再组合起来。

stable diffusion：
论文地址：http://arxiv.org/abs/2112.10752

该模型也是三块，与刚才说的三个组件对应起来。如1号编码器，不过它的输入不仅有文字，还有图片等。2号生成器。3号解码器。

DALL-E系列：
论文地址：
http://arxiv.org/abs/2204.06125
http://arxiv.org/abs/2102.12092

该模型也是三块，与刚才说的三个组件对应起来。三招鲜。
1号编码器，编码文字；
2号生成模型试了两个，autoregressive自回归，因为输入已经是先做了一些处理以后的，而且也不用一下子生成完整图片（不然运算量太大），只是生成图片的压缩版本，所以也许用自回归的方法还可以。其次也可以用扩散Diffusion model。
最后3号decoder。

Imagen
谷歌公司提出的。http://imagen.research.google/
论文地址：
http://arxiv.org/abs/2205.11487

还是三招鲜套路。1号文本编码器；但2号输出的就已经是人类能看懂的图片了，不过是很小的图片，64✖64的。然后通过3号解码器输出1024✖1024的大图。

下面我们学习这三招鲜里面的细节。

Text Encoder

可以用GPT，bert等作为文字text encoder。

看下图：10K张图片，用了FID和CLIP两个指标来评价encoder的好坏。FID的值越小代表生成的图片越好；CLIP分越大越好。所以图的值越往右下角越好。
（a)图几条线之间有差距，说明这个文字的encoder对最后的结果影响很大。
（b)图U-net size就是指Diffusion里的Noise prediction 的大小。说明增大Diffusion模型，对结果的帮助是比较有限的。

FID（Frechet Inception Distance），弗雷歇感知距离：
http://arxiv.org/abs/1706.08500

用来度量生成图像的好坏。
就是一个预训练好的CNN分类模型，把真实图片和生成的图片丢进去，CNN的输出就是隐层representation。把真实图片的representation（红点）和生成图片的representation（蓝色）画出来，这两组数据越接近就说明生成的图片和真实图片越接近。
那怎么度量这两组数据representation的距离呢？FID用的是一个很粗糙但很有用的方法，就是假设这两组representation都是高斯分布，然后计算这两个高斯分布的弗雷西frechet距离，值越小越好，和人类主观评估较为一致。

但FID有一个问题，就是需要采样大量的图片。比如上面需要10K张。

CLIP（Contrastive Languange-Image Pre-Training）:
https://arxiv.org/abs/2103.00020
用400million的图像-文本的成对资料。
把文本和图像分别输入Encoder，如果是成对的，就希望输出向量的距离更近，反之更远。

Decoder

训Decoder不需要图片-文本的成对资料，单凭大量的图片就能训练。

具体怎么训呢？

• 如果“中间产物”为小图：把图片都下采样成小图，小图-原图，这就有成对资料啦。
  

• 如果“中间产物”为隐层表示Latent representation：训一个自编码器Auto-encoder即可。将图片输出Encoder，得到Latent representation，再输入Decoder，还原为原来图片，让输入和输出越接近越好。训练完后，直接把Decoder拿出来用就行了。
  再讲详细一点，举个例子，比如输入的是H✖W✖3的图片，Encoder输出Latent representation为h✖w✖c尺寸，可以看作是一张小图，只不过是人类看不懂的小图，可能是下采样的结果，如h=H/10，w=W/10，c代表channel。
  

Generation Model

最后来看Generation Model。它的作用是输入文字的representation和杂讯，输出“中间产物”。

那具体怎么训呢？
之前在做diffusion process的时候，你的Noise是加在图片上，但现在我们是将Noise加在“中间产物”上或latent represatation上。
现在，我们假设“中间产设”就是latent represatation，那做法就是，将图片输入一个Encoder，输出一个latent represatation，采样一个与latent represatation维度一样的杂讯，加在latent represatation上面，就得到一个稍微有杂训的latent represatation，再采样一个杂讯加上面，又变一点…以此类推，直到最后加了够多的杂讯，你的latent represatation也成了从杂讯采样出的样子。

接下来，再训一个Noise predictor，这跟训一般的Diffusion Model一模一样。输入文字向量、加杂讯的latent represatation，第几步（所有蓝框部分）,输出预测的Noise（红框部分）。

在生成图片的时候，做法就是如下图：
从高斯分布中采样出来的latent represatation，它的大小的就是一个小图的样子，把它和一段文字输入denoise model，输出的latent represatation就去掉了一些noise，再输入Denoise…以此类推，直到一定次数之后，你觉得产生的结果够好了，就把这个结果输入到Decoder，输出就是图片。

Diffusion Model生图的话，一开始你会看到完全random的杂讯，白噪声，就像电视坏掉那样，然后噪声越来越少，然后图才生出来。但是Mijourney，它生图的时候不是这样，你会发现它是从一张模糊的，看得清大概轮廓的图，然后越来越清楚，中间可能还会产生某个部件然后画到最后还会不见了这样。为什么这样呢？因为它是把每次Denoise输出的latent representation通过Decoder后变成图给你看， 比如一开始我们输入的是完全从高斯分布采样出的latent representation，把它输入Decoder，也会输出一张比较模糊的图，而不是像有噪声加在上面。这就是为什么Mijourney的中间产物也是人能看得出来是什么东西的图，其实就是把中间产物又通过一次Decoder后展现的。

数学原理

现在我们已经学习了Diffusion Model的基本概念，非常直观好理解。那接下来就学习他背后的数学原理。

引言

首先，我们先回忆一下Diffusion Model的基本概念。前向过程，或叫Diffusion process，就是一张图片，不断加Noise，知道你看不出来这张图片原来的样子。反向过程就是给它一张全是noise的图片，不断Denoise，图像一点点出来，直到出来一张完整清晰的图片。

VAE和Diffusion Model的比较
VAE模型和Diffusion模型非常相似，我们可以看看它们的异同。
VAE就是把图片输入Encoder，输出latent representation，再输入一个Decoder，让还原回图片。
Diffusion里的N次加噪Add noise和N次去噪Denoise的过程，就像encoder和decoder过程。只不过Add noise的过程不是神经网络learn出来那种，而是人为设计固定好的。加噪后完全的杂讯图就类似VAE中的latent representation。

我们再来看一下原始论文中的算法：

其实暗藏玄机！
如果你仔细读一下这个算法，就会发现似乎和我们讲的概念不太一样。

那我们一起读一下这个算法：
算法1 Training:
1.重复; 6.直到收敛。就是一直重复2-5行的事情直到收敛。
2.x0就是从你收集到的数据库里拿出的一张干净的图
3.T可能会是一个比较大的数，如1000。就是从1-1000里采样一个数字
4.ε就是杂讯图，从标准正太分布里采样出来的
5.先看红色框框里，代表的就是一张带杂讯图，就是把x0和ε做加权求和，它们的权重为α1，α2，…，αT的bar，权重都是事先定好的。
εθ就是Noise predictor，输入噪声图片和t。求的就是杂讯图减去预测的杂讯。

然后输入Noise predictor：

这个就是DDPM真正做的事情，但回忆之前我们讲的，你就会发现优点不太一样，之前是个概念性的讲法，就是想象中，一张图片给它一点点加上噪声，最后又从噪声图还原回原来的图。然而实际上，DDPM的算法的做法是干净的图直接混入一个噪声，用前面的权重决定它们的比例，混入噪声的大小，得到带噪图，最后输入带噪图，去预测噪声。这个过程并不是想象中把噪声一点一点加进去的，而是一次性加进去，Denoise也是一次就给预测出来噪声。

Inference:
1.先采样一张全是杂讯的图xT
2.循环3和4步骤T次
3.又采样一次噪声（为什么再采样一次噪声呢？后面会讲解）
4.这个公式比较复杂，下面用图的形式表现出来了
εθ就是Noise predictor，εθ(xt,t)即输入全杂讯图和step，输出预测的噪声，乘以一个权重，用原图xt减去预测到的噪声，得到去噪的图，还得乘以个权重，按理说这样就结束了，然后再加一个z噪声。

为什么还要加一个噪声z呢？
这我们就得从图像生成模型本质上的共同目标说起。

今天，所有的图像生成模型本质共同的目标都是：
输入是一个简单的分布（如高斯分布，可以均值为0，每个维度方差为1），从里面采样一个向量出来，输入网络G，得到ｘ＝Ｇ(z)，输出x就是一张图片。每次从这个简单的分布采样一个点，通过网络就可以变成一张图片，输出的这些图片就可以组合成一个复杂的分布。我们期待是能找到一个网络，使得输出的分布和真正想要的目标图片分布越接近越好。

今天更常见的应用是输入一段文字，生成图片。但原理上和刚才一样，只是多加了一段文字作为条件condition。
文字一句话“一只奔跑的狗”，可以生成不同的奔跑狗的图片。所以学习目标就是学到奔跑狗图片的分布。

加了文字，但原理上并没有本质的差异，所以下面的内容为了数学式更简洁一点，就先假设没有文字condition的输入。但实际应用的时候，加上文字并不会影响你的演算法。

我们希望生成的数据分布和目标分布越接近越好，那怎么衡量两个分布之间的接近程度呢？
多数图像生成任务采取的是最大似然估计。原理如下：
假设网络参数为θ，生成的数据分布Pθ(x)，真实数据分布Pdata(x)，Pθ(xi)也就是通过这个网络，产生出图片i的概率，实际可能很难计算出Pθ(xi)，因为Pθ(x)非常复杂，不是简单的高斯分布，而是一个非常复杂到你难以想象的分布。
但现在咱们先假设能算出Pθ(xi)。最大似然估计就是将你采样的图{x1, x2 ,…, xm}，计算产生这些图片xi的概率Pθ(xi)，全部相乘，找到一个θ让乘积越大越好，乘积最大时的那个θ，我们叫作θ*，也就是我们训练网络的参数。

那让Pθ(xi)的乘积越大越好，和让Pθ(x)和Pdata(x)越接近有什么样的关系呢？
1.把上面那个式子，前面取个log，这个不会影响我们最终求的结果
2.logAB=logA+logB，乘变加，最后相当于算期望
3.多加一项含有logPdata(x)，对结果没影响，只是为了凑个KL散度

KL值越大，代表两个分布的差异越大，反之亦然。
最大似然估计=最小KL散度， 这就是所有的图像生成模型本质共同的目标。
生成模型中，像VAE、flow_based、diffusion mode它们都是用最大似然估计，而GAN就是最小化某个散度，但不是KL散度，最原始的GAN是最小化JS散度，你也可以修改成KL散度形式，但做出来效果不会更好。

回顾VAE

VAE：计算Pθ(x)
我们又再回忆一下VAE（详细看我之前博客），因为VAE和difussion model非常类似，很多在VAE中推导过的公式，在diffusion model中就不用再推导一次了。

z是从简单分布（如高斯分布）中随机采样的一个点，输入网络，生成数据x。

生成的数据分布Pθ(x)，所以P(z)已知如高斯分布，但Pθ(x|z)怎么算呢？

Pθ(x|z)可以写成：

那这样算有可能结果几乎都是0。因为生成的图片G(z)和真实图片x不可能完完全全一样，按这个定义如果有一两个像素pixel有差异G(z)≠x，它的概率就等于0。

所以，在VAE中是这么假设的：
假设输入一个z，输出的G(z)代表的是一个高斯分布的均值。

那么，可以得到：
Pθ(x|z)和exp(-||G(z)-x||2)成正比。

直觉上也能看出，如果G(z)和x越接近，值越大，即Pθ(x|z)越大。

VAE：logP(x)的下界
注明一下，后面就把Pθ(x)简写成P(x)，就是代表需要网络的参数θ算出来的。
1.根据贝叶斯公式：P(x)=P(z, x)/P(z|x)。然后多加一项
2.logAB=logA+logB，乘变加
3.后面一项变成KL散度，该项≥0
4.最后推导下界用期望表示，q(z|x)就是Encoder。

DDPM

计算Pθ(x)

上面一行是denoise的过程
下面一行，你把denoise 的输出也想象成是一个高斯均值。

某张图片x0被产生出来的概率（x1:xT表示x1一直到xT）：

有同学问：

• t和T什么关系？
  t是0-T之间的某个数。
• 除了高斯分布，可以是别的分布吗？
  可以的，或者其他更复杂的假设，高斯假设就更简单一些。而且我们只考虑了高斯分布每个维度的均值为1，还没有考虑方差，其实也可以把方差考虑进来，但是过去的文献表明考虑方差做出来也没多好。
• 为什么第一个P(xT)没有下标θ，其他的都有θ？
  因为第一个是从一个已知分布(高斯分布)中采样出来的，其他的都是通过神经网络训出来的，网络参数为θ。接下来的内容可能Pθ(x)简化成了P(x)，哪些是简化，哪些是有意义，大家要自己判断一下。

DDPM：logP(x)的下界
DDPM的下届，推导和VAE一样，这里就不再赘述，唯一的不同就是x换成x0，z换成x1:xT。VAE的q(z|x)就是Encoder，而DDPM的q(x1:xT|x0)就是前向过程，即加noise的过程。

—> 计算q(x1:xT|x0)：

那里面的每一项q(xt|xt-1)怎么算呢？
β是事先准备好的，这个东西有点像神经网路的超参数，可以调参。
可以看出q(xt|xt-1)还是一个高斯分布，均值是右边第一项，方差是第二项。

—> 计算q(xt|x0)：
想象中，好像是先产生x0，再产生x1,…,一直到xt。

但实际，q(xt|x0)是可以直接被计算出来的。
看下图，是x1和x2的计算过程，每次从高斯分布N(0,I)中采样相互独立。红框部分就是x1，可以代入到下式的x1部分。

就可以得到：

那么，从一个高斯分布中采样两次，再乘以不同的权重，把它们加起来（红框部分），可以简化成看作只采用一次，乘以一个它们权重之和。

那么，x2就等于如下：

有同学问：
之前做t次高斯分布采样，现在就做一次可以吗？
t次高斯分布采样都是相互独立，现在做一次的结果是一样的。

为了简化符号，我们定义：

以此类推，整个过程可以写成：

每个子部分搞清楚了，现在回过来看看整体式子：

本来想一步步推导，但过程太长太复杂了，感兴趣的同学可以看下面那篇文章。

总之，经过一番推导后，就得到最下面的式子：
也就是最大化该式。第二项不用管，因为和网络的参数θ无关，你看P(xT)就是从高斯分布中采样出来的全是杂讯的图片，q(xT|x0)是diffusion process，是人工定好的，和网络也完全没有关系。

再看第一项和第三项，它们计算过程非常像，所以接下来我们只讲第三项的计算。

—> 计算q(xt-1|xt,x0)：

我们回忆一下，上面我们学了这三个东西的计算：

但并不会算q(xt-1|xt,x0)，怎么办呢？
先看看这个式子是代表什么含义呢：假设已知x0和xt，就是给了一张x0，做了t次diffussion得到xt，但是中间过程看不见，问你xt-1长什么样？

我们可以把q(xt-1|xt,x0)经过一番拆解化简，变成我们已知会算的东西的组合（利用贝叶斯和条件概率等公式）：
而且已知的这三项都是高斯分布，它们的均值方差也都知道

接下来的推导也很多，感兴趣可以看下面链接文章。

经过上面一堆硬推之后，发现得到的结果也是高斯分布的，它的均值和方差如下：

现在，要做的就是最小化它们的KL散度。

它们两都是高斯分布，而两个高斯分布的KL散度是有公式解的：

但是，有更简单的计算方法，或者说我们并不需要实际把KL散度算出来，因为我们目的是最小化KL散度就行。

—> q(xt-1|xt,x0)，橘色圈：
这个高斯分布的均值和方差是固定的，因为它和网络没任何关系，它的diffudion process是人工设定好的。
—> p(xt-1|xt)，蓝色圈：
是由网络denoise model决定的，但它的方差是固定的(也有文献讨论过它，即使考虑方差效果也好不了多少)，所以只考虑均值。
橘色圈中心（均值）和半径（方差）都是固定的，蓝色圈的中心固定，圈圈半径不固定，那现在我们要这两个高斯分布的越接近，就是让它两的中心越接近越好，即均值越接近越好。

实际操作就是：
橘色圈的均值知道，蓝色圈的均值是从Denoise model输出来的。所以我们做的事情就是训练Denoise model，让输出的结果和橘色圈越接近越好。

E下面还有一个式子q(xt|x0)，回忆一下：

所以xt和x0之间的关系是：

经过挪项，也可以得出x0，用xt的表示：

现在我们要做的事情是，输入xt和t，希望输出和这个均值越接近越好，但可以看到右边这个均值里面没有xt-1，所以不需要把xt-1考虑进来。

把刚才的x0代入该式，得到：

所以，实际上denoise model需要输出的目标是如下：
输出目标中，只有ε是需要网络预测的部分，其他都是常数，在训练前都设定好的参数。

这就和论文中的算法一样了：

有同学问：
如果参数α也训练呢？
其实DDPM论文也有写，他们试图训过α，但是结果提升不大，所以之后都不管α了。

讲到这里，还有一个没有解决的问题，就是为什么后面多加一项noise，σz.

你可能会说，既然Denoise model 的输出就是一个高斯分布的均值，那做采用的时候再加一个noise，正好可代表方差。

那我们在inference的时候，为什么不直接取均值呢？
因为直接取均值代表是取高斯分布的概率密度的最大值，这样不也是很合理吗？李宏毅老师在文献上还没有找到很好的答案，下面只是个人猜测，不一定对，大家听听就好。

同样的问题，你也可以问：为什么语言模型在生成文句时需要采样？

为什么要先产生一个分布，再从这个分布中采样出这个文字呢？为什么不直接取概率最大的那个输出就行呢？可能有人会说，比如采样的好处就是每次输入同一个问题，ChatGTP每次回答的都不一样。那每次让它回答一样的答案不好吗？就是说输出固定不好吗，为什么要有随机性？

其实这个问题以前有人研究过，下面这篇文章就是就GTP2上研究的。研究发现，如果每次取概率最大的句子或词汇，机器每次输出的就会是不断重复的句子，机器就会开始不断地跳帧，讲重复的话。虽然你做采样sampling，机器会输出好像奇奇怪怪的话，但是跟跳帧比起来，感觉结果更好。

作者做了个分析，右边是人写的文章（图中橙色线），左边是机器写的（蓝色）。根据我们用语言模型计算人写的这篇文章中每一个字出现的概率，你会发现人写词每次用词不一定是出现概率最大的词，但机器每次产生概率最大的词，所以机器写的文字都在重复一样的话，不断地跳帧。在做生成任务时，概率最大地输出并不一定是最好地。

---

同样的问题，你也可以问：为什么语音合成时也需要采样呢？

今天语音合成地模型都是用端到端模型硬train的，输入一段文字，输出一段声音。这个发展也很早，比如下面这是来自2017年的tacotron一篇文章。

其实很早的时候，李老师实验室也一直尝试做端到端的语音合成TTS模型，但很长一段时间做不起来，后来有个谷歌的人说了一个tips：就是在推理的时候加入dropout！！！

我们知道一般在训练，或者过拟合的时候我们才会加dropout，按理测试或推理时不该加dropout，但是没想到TTS任务中，推理的时候加上dropout一下就做起来了。 没加dropout的声音就全是噪声，有点像机关枪一样，完全没有人声（我之前复现一篇语音转换VC论文时也是这样的声音，当时还不明白为什么会这样），它和产生句子时选择概率最大，不断跳帧是一样的。但是加上dropout时，就是正常人声了。

---

现在再来看Diffusion model，会不会也是同样的道理呢？

Diffusion model也是一种自回归模型，是自回归模型和非自回归模型众和妥协的结果，也就是说非自回归模型是“一次到位”，但通常产生的结果不够好，我们可以变成“多次到位”，这就是Diffusion model的概念，每一次做Denoise的时候，就好像自回归模型中的一个step，既然在做自回归模型时，我们要加一点noise，加一点随机性， 结果才会好，所以也许在做Denoise的时候，我们就要加一点随机性结果才会好。

为了验证这个说法，因此也做了一个实验，如果σ=0，压根合不出图，如果σ按照人家论文设置，才会出来图。

扩散模型的应用及优点

在语音上：
Diffusion model不是只能用在图片任务中，在语音上也有应用。比如，用在语音合成TTS任务上，原理和在在图片上一模一样。就是把输入二维的图片，换成一维的语音。你从一个完全高斯分布采样的杂讯，然后一步步denoise，最后变成语音信号。

今天比较知名的方法：WaveGrad，原理基本上和DDPM没什么差别。就只是把输入从二维噪声换成一维噪声。

在文本上：
Diffusion model用在文字上，有点麻烦，不能直接应用DDPM，因为你看啊，输入是图片或语音的时候，一直加高斯噪声，直到完全变成只有高斯的噪声，而文字是离散的，没办法把一个离散的东西一直加噪声，变成完全高斯的噪声。

不过人们也想出了解法：
1.把噪声加在隐空间，如word Embedding。

现在知名的模型如：

• Diffuion-LM
  

• DiffuSeq
  

2.另一种解法就是，既然高斯噪声不能加在文字这种离散的东西上，那加别的种类的噪声呢？
有一系列的工作，如有加mask的。

Diffusion model成功的关键：
"一次到位"改成“N次到位“。就是把自回归模型的优势，加到了非自回归里。

其他类似思想

过去其实也有这方面文章，就是把非自回归的模型改成自回归模型，你就可以得到很好的结果。这些文章的精神和Diffusion model 很像，就是他们在论文里并没有提到最大似然估计等等这些数学式，但是他们也得到了很好的结果。比如如下模型。

Mask-Predict
这个方法在很多地方都有用到，所以不一定叫mask-predict。

在NLP任务上：
比如一个问答机器人，Encoder输入”请问李宏毅的职业是什么？“，现在有两个答案，演员和老师。如果Decoder是个非自回归模型，即一次到位的模型，输入给Decoder一串mask，它只输出概率最大的，比如，第一个字其实”演“和”老“字的概率都很大，但它选了最大的”老“字，第二个输出概率最大的是”员“字，最后结果输出就i是”老员“，所以结果很不好。怎么办呢？

就用mask-predict方法：
如果第一次输出结果不太好，那就再做第二次。把输出的结果里面，概率比较低的mask掉，比如上图”老“概率0.3最低，用mask盖住，再输入一次Decoder，重新再做一次结果的生成，这次”员“是直接给定的，所以这个mask的地方就很有可能是”演“，就可以解决非自回归模型举棋不定的问题。这就相当于在另外一个方向上又做了自回归，就可以解决只做非自回归的劣势。

---

在图像任务上：
Masked Visual Token Modeling(MVTM)

先训一个autoencoder。

输入一张图片，在Encoder输出的中间隐变量code上，把一些地方mask掉，也就是把上面的一些token换成mask的token，然后再训练一个模型，就是让模型把mask掉的地方再猜回来。

那训练完后，在推理阶段的做法就是：
一开始，图片全部都是被mask的，丢入Decoder，输出一张图片，把这张产生的图片里概率数比较低的部分，再mask盖掉，再输入Decoder，重新生图…一直重复，直到产生很好的结果。

下面是论文里展示的模型生成图的过程：
先看第一行，从左边开始，一开始图片一片灰色，代表全被mask，然后把它丢到Decoder里面，产生第二张图，可能很多confident都很低，所以只有一个点token被保留下来。然后再输入Decoder，重复这个过程，可以看到可信token点保留的越来越多。
我们把每次生成的token都丢到Decoder1(注意：这个Decoder1和Decoder不是同一个解码器，所以我后面标个1)，为了生成可视化的图片，让我们知道每步的过程的图片长什么样，可以看到产生的图片越来越清晰。Decoder是在产生新的token，Decoder1是产生可视化图片。

上面的这种文章，他们都是自称非自回归的，是自回归还是非自回归，你得看是相对于谁讲，相对于直接把产生这些token当作一个语言模型，直接训一个GPT，那上面这种就是非自回归的；相较于过去你一次把图片就产生出来的非自回归模型，上面这种就是加入了自回归的特色的模型。

纯自回归的模型，生图片的时候的token就是一个一个按顺序生出来的，要花非常长的时间（上图最后t=7，下图t=255），不过产生的图也会很清晰。

所以，把自回归的特色，加入到非自回归模型里，相当于把两种模型的优势结合起来，只用比较少的迭代次数，就可以产生和纯自回归模型一样好的结果，因为它不像纯自回归一次只产生一个token，而是一次产生一堆token。

最后谷歌有篇也是做图片生成的，号称比diffusion model做的更好，但它其实就是用这种mask predict的方法，没有用diffusion model，看起来有没有用diffusion model可能也没有那么重要，而是把自回归的思想加入非自回归的优势最重要。