GAN | 代码简单实现生成对抗网络(GAN)(PyTorch)
GAN从编程的角度来看(纯个人理解,不对可指正)利用numpy的random方法,随机生成多维的噪音向量创建一个G网络用来生成创建一个D网络用来判断俩个网络在训练时分别进行优化先训练D网络去判断真假:如果训练D为真时,进行传播;如果训练D为假时,进行传播,投入优化器(1为真,0为假)在D的基础上训练G。*因为是随机生成,所以每次生成结果不同。
·
2014年GAN发表,直到最近大火的AI生成全部有GAN的踪迹,快来简单实现它!!!
GAN通过计算图和博弈论的创新组合,他们表明,如果有足够的建模能力,相互竞争的两个模型将能够通过普通的旧反向传播进行共同训练。
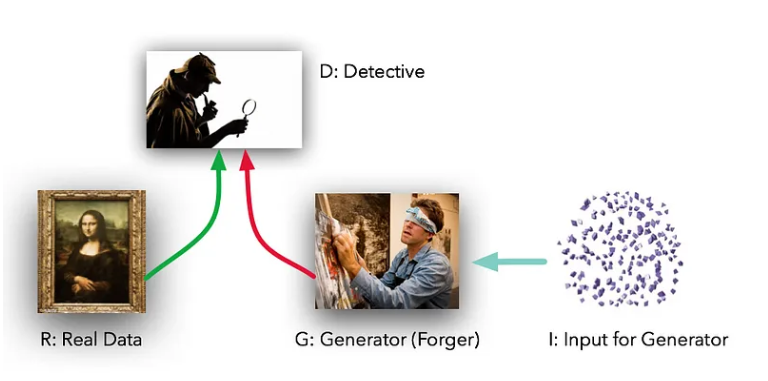
这些模型扮演着两种不同的(字面意思是对抗的)角色。给定一些真实的数据集R,G是生成器,试图创建看起来像真实数据的假数据,而D是鉴别器,从真实集或G获取数据并标记差异。 G就像一造假机器,通过多次画画练习,使得画出来的话像真图一样。而D是试图区分的侦探团队。(除了在这种情况下,伪造者G永远看不到原始数据——只能看到D的判断。他们就像盲人摸象的探索伪造的人。

GAN实现代码
#!/usr/bin/env python
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
from torch.autograd import Variable
matplotlib_is_available = True
try:
from matplotlib import pyplot as plt
except ImportError:
print("Will skip plotting; matplotlib is not available.")
matplotlib_is_available = False
# Data params
data_mean = 4
data_stddev = 1.25
# ### Uncomment only one of these to define what data is actually sent to the Discriminator
#(name, preprocess, d_input_func) = ("Raw data", lambda data: data, lambda x: x)
#(name, preprocess, d_input_func) = ("Data and variances", lambda data: decorate_with_diffs(data, 2.0), lambda x: x * 2)
#(name, preprocess, d_input_func) = ("Data and diffs", lambda data: decorate_with_diffs(data, 1.0), lambda x: x * 2)
(name, preprocess, d_input_func) = ("Only 4 moments", lambda data: get_moments(data), lambda x: 4)
print("Using data [%s]" % (name))
# ##### DATA: Target data and generator input data
def get_distribution_sampler(mu, sigma):
return lambda n: torch.Tensor(np.random.normal(mu, sigma, (1, n))) # Gaussian
def get_generator_input_sampler():
return lambda m, n: torch.rand(m, n) # Uniform-dist data into generator, _NOT_ Gaussian
# ##### MODELS: Generator model and discriminator model
class Generator(nn.Module):
def __init__(self, input_size, hidden_size, output_size, f):
super(Generator, self).__init__()
self.map1 = nn.Linear(input_size, hidden_size)
self.map2 = nn.Linear(hidden_size, hidden_size)
self.map3 = nn.Linear(hidden_size, output_size)
self.f = f
def forward(self, x):
x = self.map1(x)
x = self.f(x)
x = self.map2(x)
x = self.f(x)
x = self.map3(x)
return x
class Discriminator(nn.Module):
def __init__(self, input_size, hidden_size, output_size, f):
super(Discriminator, self).__init__()
self.map1 = nn.Linear(input_size, hidden_size)
self.map2 = nn.Linear(hidden_size, hidden_size)
self.map3 = nn.Linear(hidden_size, output_size)
self.f = f
def forward(self, x):
x = self.f(self.map1(x))
x = self.f(self.map2(x))
return self.f(self.map3(x))
def extract(v):
return v.data.storage().tolist()
def stats(d):
return [np.mean(d), np.std(d)]
def get_moments(d):
# Return the first 4 moments of the data provided
mean = torch.mean(d)
diffs = d - mean
var = torch.mean(torch.pow(diffs, 2.0))
std = torch.pow(var, 0.5)
zscores = diffs / std
skews = torch.mean(torch.pow(zscores, 3.0))
kurtoses = torch.mean(torch.pow(zscores, 4.0)) - 3.0 # excess kurtosis, should be 0 for Gaussian
final = torch.cat((mean.reshape(1,), std.reshape(1,), skews.reshape(1,), kurtoses.reshape(1,)))
return final
def decorate_with_diffs(data, exponent, remove_raw_data=False):
mean = torch.mean(data.data, 1, keepdim=True)
mean_broadcast = torch.mul(torch.ones(data.size()), mean.tolist()[0][0])
diffs = torch.pow(data - Variable(mean_broadcast), exponent)
if remove_raw_data:
return torch.cat([diffs], 1)
else:
return torch.cat([data, diffs], 1)
def train():
# Model parameters
g_input_size = 1 # Random noise dimension coming into generator, per output vector
g_hidden_size = 5 # Generator complexity
g_output_size = 1 # Size of generated output vector
d_input_size = 500 # Minibatch size - cardinality of distributions
d_hidden_size = 10 # Discriminator complexity
d_output_size = 1 # Single dimension for 'real' vs. 'fake' classification
minibatch_size = d_input_size
d_learning_rate = 1e-3
g_learning_rate = 1e-3
sgd_momentum = 0.9
num_epochs = 5000
print_interval = 100
d_steps = 20
g_steps = 20
dfe, dre, ge = 0, 0, 0
d_real_data, d_fake_data, g_fake_data = None, None, None
discriminator_activation_function = torch.sigmoid
generator_activation_function = torch.tanh
d_sampler = get_distribution_sampler(data_mean, data_stddev)
gi_sampler = get_generator_input_sampler()
G = Generator(input_size=g_input_size,
hidden_size=g_hidden_size,
output_size=g_output_size,
f=generator_activation_function)
D = Discriminator(input_size=d_input_func(d_input_size),
hidden_size=d_hidden_size,
output_size=d_output_size,
f=discriminator_activation_function)
criterion = nn.BCELoss() # Binary cross entropy: http://pytorch.org/docs/nn.html#bceloss
d_optimizer = optim.SGD(D.parameters(), lr=d_learning_rate, momentum=sgd_momentum)
g_optimizer = optim.SGD(G.parameters(), lr=g_learning_rate, momentum=sgd_momentum)
for epoch in range(num_epochs):
for d_index in range(d_steps):
# 1. Train D on real+fake
D.zero_grad()
# 1A: Train D on real
d_real_data = Variable(d_sampler(d_input_size))
d_real_decision = D(preprocess(d_real_data))
d_real_error = criterion(d_real_decision, Variable(torch.ones([1]))) # ones = true
d_real_error.backward() # compute/store gradients, but don't change params
# 1B: Train D on fake
d_gen_input = Variable(gi_sampler(minibatch_size, g_input_size))
d_fake_data = G(d_gen_input).detach() # detach to avoid training G on these labels
d_fake_decision = D(preprocess(d_fake_data.t()))
d_fake_error = criterion(d_fake_decision, Variable(torch.zeros([1]))) # zeros = fake
d_fake_error.backward()
d_optimizer.step() # Only optimizes D's parameters; changes based on stored gradients from backward()
dre, dfe = extract(d_real_error)[0], extract(d_fake_error)[0]
for g_index in range(g_steps):
# 2. Train G on D's response (but DO NOT train D on these labels)
G.zero_grad()
gen_input = Variable(gi_sampler(minibatch_size, g_input_size))
g_fake_data = G(gen_input)
dg_fake_decision = D(preprocess(g_fake_data.t()))
g_error = criterion(dg_fake_decision, Variable(torch.ones([1]))) # Train G to pretend it's genuine
g_error.backward()
g_optimizer.step() # Only optimizes G's parameters
ge = extract(g_error)[0]
if epoch % print_interval == 0:
print("Epoch %s: D (%s real_err, %s fake_err) G (%s err); Real Dist (%s), Fake Dist (%s) " %
(epoch, dre, dfe, ge, stats(extract(d_real_data)), stats(extract(d_fake_data))))
if matplotlib_is_available:
print("Plotting the generated distribution...")
values = extract(g_fake_data)
print(" Values: %s" % (str(values)))
plt.hist(values, bins=50)
plt.xlabel('Value')
plt.ylabel('Count')
plt.title('Histogram of Generated Distribution')
plt.grid(True)
plt.show()
train()代码输出结果


个人总结
GAN从编程的角度来看(纯个人理解,不对可指正)
利用numpy的random方法,随机生成多维的噪音向量
创建一个G网络用来生成
创建一个D网络用来判断
俩个网络在训练时分别进行优化
先训练D网络去判断真假:如果训练D为真时,进行传播;如果训练D为假时,进行传播,投入优化器(1为真,0为假)
在D的基础上训练G。
*因为是随机生成,所以每次生成结果不同
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容








所有评论(0)