
(四)BP神经网络预测(上)
BP神经网络适用于机器人控制、组合优化、模式识别、图像信息处理,能够对非线性数据建立精确的模型,对其未来进行预测。其核心思想是:将已预处理好的数据放到神经网络的微分方程进行反复训练,通过大量的训练建立BP神经预测模型,在此基础上再对其他数据进行预测。.........
BP神经网络适用于机器人控制、组合优化、模式识别、图像信息处理,能够对非线性数据建立精确的模型,对其未来进行预测。其核心思想是:将已预处理好的数据放到神经网络的微分方程进行反复训练,通过大量的训练建立BP神经预测模型,在此基础上再对其他数据进行预测。
每次算法训练的过程由信息的正向传播和误差的反向传播两个过程组成,输入层各神经元负责接收来自外界的输入信息,并传递给中间层各神经元;中间层是内部信息处理层,负责信息变换,根据信息变化能力的需求,中间层可以设计为单隐层结构或者多隐层结构;最后隐层把信息传递到输出层各神经元,完成一次训练的正向传播处理过程,由输出层向外界输出信息处理结果。当实际输出与期望输出的误差没有达到设定的指标时,进入误差的反向传播阶段。误差通过输出层,按误差梯度下降的方式修正各层权值,向隐层、输入层逐层反传。周而复始的信息正向传播和误差反向传播过程,是各层权值不断调整的过程,也是神经网络训练的过程,此过程一直进行到网络输出的误差减少到设定的最小误差范围内,或者到达预先设定的训练次数为止。(源于CSDN:(17条消息)【神经网络】采用BP神经网络模型进行预测的主要思想是_Borter-CSDN博客_bp神经网络预测模型)
对一定的样本数据(输入与期望输出)进行学习,即样本的输入送至网络输入层的各个神经元,经过隐层的和输出层的计算后输出,输出层的各个神经元输出对应的预测值。若预测值与期望值之间的误差不满足精度的要求,则从输出层反向传播该误差,从而进行权值和阈值的调整,是的神经网络的预期输出与期望输出之间的误差逐渐减小,直到满足精度要求(MATLAB智能算法30个案例分析(第2版),郁磊,史峰,王辉,胡斐,第25章,基于神经网络的回归拟合)
数据预处理

将数据集导入matlab进行归一化处理,调用premnmx()函数进行归一化。
模型的建立
我们对BP神经网络的权值和阈值的公式进行详细的推导:


模型的求解

1、这是神经网络的一个界面,这是一个2输入1输出,5个隐含层的BP网络,称为2-5-1网络结构(另外输入、隐层、输出的数量可以根据实际情况自行调整)

2、参数的解读

(1)泛化性:表示BP神经网络在训练过程中,如果均方误差(MSE)连续6次不降反升,则网络停止训练
(2)误差精度:关于mu参数含义的一种理解是,mu是误差精度参数,用于给神经网络的权重再加一个调制,这样可以避免在BP网络训练的过程中陷入局部最小值,mu的范围为0到1。

横坐标:训练结束时的epochs数【神经网络一次前向传播+一次反向传播=一个epoch】
纵坐标:均方误差
从图中可以得到:在epochs=5时,验证集valiadation和测试集test达到最小均方误差。

训练集
横坐标:epoch
纵坐标:梯度gradient;
梯度:若梯度为0,则为图像最低点,即最优位置
mu:
valfail:
【validationcheck=6:若连续六次训练,训练误差没有变小,则假定继续训练下去效果不会变好,停止训练。】

误差直方图
横坐标:误差区间的中位数;
纵坐标:位于该误差区间的样本个数
可以得到:神经网络的输出值与样本原目标值的误差;

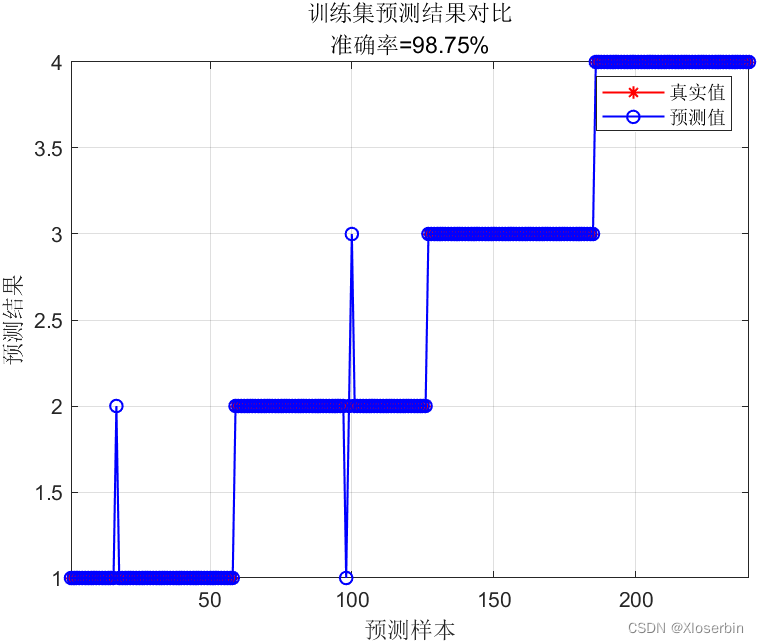
预测值和目标值的线性化程度
横坐标:样本原目标值;
纵坐标:神经网络输出预测值;
可以得到:原目标值和预测值的相关度;用系数R表示,若R越接近1,则表示线性化程度越高,结果越好。
结果分析到结论分析
| 总结图像分析: (1)预测值和真实值、误差的分析图像 (2)训练集、验证集、测试集和总体的均方误差随训练次数的变化图像 (3)BP神经网络各阶段的训练图像 (4)各个样本集和总体的相关性分析图像 (5)训练集、验证集和测试集的误差分布直方图像 |
模型的改进
过拟合:模型参数拟合过程中,由于训练数据包含抽样误差、训练时,复杂的模型将抽样误差也考虑在内,将抽样误差也进行了很好的拟合。具体表现就是模型在训练集上效果好,在测试集上效果差,模型泛化能力弱。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容








所有评论(0)