BP神经网络结构解说
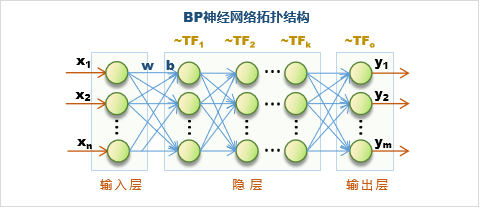
BP神经网络的通用结构如下：


它属于前馈型神经网络，结构具体解说如下
1. 网络层数：共包括三大功能层：输入层、隐层和输出层
其中隐层可以包含多个子层
2. 神经元个数：输入层的神经元个数就是输入的个数
隐层的神经元个数自行设定
输出层的神经元个数就是输出的个数
3. 网络权重：每层的神经元都与后一层神经元用权重一一连接
4. 神经网阈值：隐层和输出层每个神经元都有自己的阈值
5. 激活函数：隐层和输出层都有自己的激活函数

✍️关于结构中的待定参数
以上仅是一个通用的结构形式，
在使用时，我们需要设定具体的参数，让它有具体的结构
需要确定的参数有以下：
👉 隐层个数
👉 每个隐层的隐神经元个数
👉 每层神经元的激活函数

1.2 常用的BP神经网络结构

虽然通用结构里允许有多个隐层，并且可以设置不同的激活函数，
但实际上,最常用的是设一个隐层
隐层神经元的激活函数设为tansig函数
输出层神经元激活函数设为purelin函数
如此一来，结构就如下图所示：



其中
tansig函数为S型函数： $\text{y} = \dfrac{2}{1+e^{-2x}} -1$
purelin 为恒等线性映射函数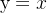： $\text{y}=x$
上图为3个隐神经元，在实际中,隐神经元个数由具体问题具体设定

✍️ 为什么实践中采用三层结构
为什么实践中一般采用上述结构呢？
主要是因为这样的结构简单又有效
简单是因为它只有一个隐层，比起多隐层网络，无疑是要简洁许多
有效是因为隐层激活函数采用了S型函数，这样网络就有了拟合非线性的能力
而输出层采用purelin，又可以让它的输出不受限制
如此一来，这种结构就“麻雀虽小，却五脏俱全”，简单又有效
后来有人证明，这种结构只要隐神经元足够，就能逼近任何函数
如此一来，基本就都使用这种结构了
✍️关于激活函数
激活函数中有两点常识，如下
1、当激活函数设为purelin时,相当于没有激活函数
2、隐层激活函数往往也可以设为logsig
logsig的表达式为 $\text{y} = \dfrac{1}{1+e^{-x}}$

它和tansig没有太多质的区别
区别只在于，logsig的取值范围是【0，1】，而tansig是【-1，1】

二. BP神经网络的工作原理

本节讲解BP神经网络的工作原理和数学表达式
通过本节，了解BP神经网络模型是如何运算的

2.1 BP神经网络的工作原理

BP神经网络的前馈机制
BP神经网络的工作原理为逐层前馈传递,如下

👉1. 先由输入层接受输入
👉2. 前馈式逐层向前传递
👉3. 最终在输出层进行输出
神经元的输入输出
神经元具体的输出输出如下所示
神经元加权累加前一层传过来的值，然后加上自身的阈值
最后经过激活函数传递给下一层各个节点

2.2 BP神经网络数学表达式

从数学表达式理解BP神经网络的机制是最直接的
下面以一个例子来说明数学表达式
网络的设置如下：
1、只设一个隐层，输入层、隐层、输出层的节点个数分别为 [2 ，3，1]
2、激活函数设置：隐层（ tansig函数），输出层（purelin函数）
则网络拓扑结构如下：
根据模型原理，
BP神经网络的数学表达式如下

表达式中参数很多，
但实际只有两类参数：权重w和阈值b
$w_{12}^{(3,2)}$ 代表这个权值是第2层的第2个节点到第3层的第1个节点的权值
$b_1^{(2)}$ 代表这个阈值是第2层的第1个节点的阈值
上标用于标示是第几层，下标用于表示是该层第几个神经元

✍️关于多层BP神经网络的表达式
对于多层BP神经网络的表达式，
只需不断按以上方式进行套娃就可以了
具体写出来过于冗长，这里将不再具体表达

三. BP神经网络的训练

本节讲解BP神经网络的训练是什么，以及主要的训练有哪些

3.1 什么是BP神经网络的训练

在BP神经网络结构确定后，模型的表达式也就确定了，
进一步我们需要确定模型里的W,b(权重阈值)
使得网络预测得最准确,也就是误差最小
关于BP神经网络的误差
BP神经网络的均方误差函数如下
$\displaystyle \displaystyle \textbf{E}(W,b)=\dfrac{1}{m}\sum \limits _{i=1}^{m} \dfrac{1}{k}\sum \limits _{j=1}^{k} (\hat{\text{y}}_{ij}-\text{y}_{ij})^2$
其中
m ：训练样本个数
k ：输出个数
$\hat{\text{y}}_{ij}$ ：第i个样本第k个输出的预测值
$\text{y}_{ij}$ ：第i个样本第k个输出的真实值
误差函数是一个关于W,b的函数，
采用不同的权重和阈值，就有不同的误差

什么是BP神经网络的训练

BP神经网络的训练，就是指求求取一组W,b，使得网络的误差最小
也即求W,b取何值时，能令上述均方误差函数\textbf{E}(W,b)最小
这个求解的过程，就称为BP神经网络的训练

3.2 BP神经网络的训练算法

对W,b的求解并不是一件容易的事情，
目前的数学水平还没有能力求得 W,b 的精确解，
通常是使用算法进行求解
BP神经网络的训练算法
BP神经网络的训练算法很多，
较经典、实用的有如下几种算法：
👉 梯度下降算法
👉 自适应学习率梯度下降法
👉 Fletcher-Reeves共轭梯度法
👉 LM算法
其中，梯度下降法是最基本，最基础的算法，
很多算法是在梯度下降法的基础上进一步改进得到

四. BP神经网络的用途

本节简单介绍一下BP神经网络怎么用，用来干什么

4.1 BP神经网络的主要用途-数值预测

在我们不知道X、y的具体关系，

而又需要用X来获取y的值的时候，
就可以使用BP神经网络来拟合X和y的关系
具体主要流程如下：

1. 采集X、y的数据
2. 设置一个合适的BP神经网络模型结构
3. 用数据训练BP神经网络的权重和阈值
4. 测试BP神经网络在新样本中的效果
5. 测试成功后，即可将BP神经网络投入使用

4.2 BP神经网络的其它用途

BP神经网络的其它用途也很多，全然靠脑洞，
在这里我们不一一举例，仅以一个例子尽下兴致
BP神经网络应用于特征提取
当我们的X变量个数很多时，
我们希望把这些变量综合成几个关键变量(也称为特征)
同时又希望综合后的关键变量尽可能包括原始变量里的关键信息
例如，语文成绩、数学成绩、英语成绩、政治成绩、历史成绩等等，
我们可以把它们综合成文科成绩、理科成绩两个特征变量
BP神经网络如何解决这问题呢？
脑洞开一下就可以了，
例如，我们要从10个变量中提取出3个特征变量，
那么只需如下设置

也就是用10个变量自己预测自己
如果训练成功，就说明3个隐节点的值已经能还原出X了
也即3个隐节点就已经包含了原本10个变量的信息了
那么我们就可以把这3个隐节点的值作为特征变量