卷积神经网络

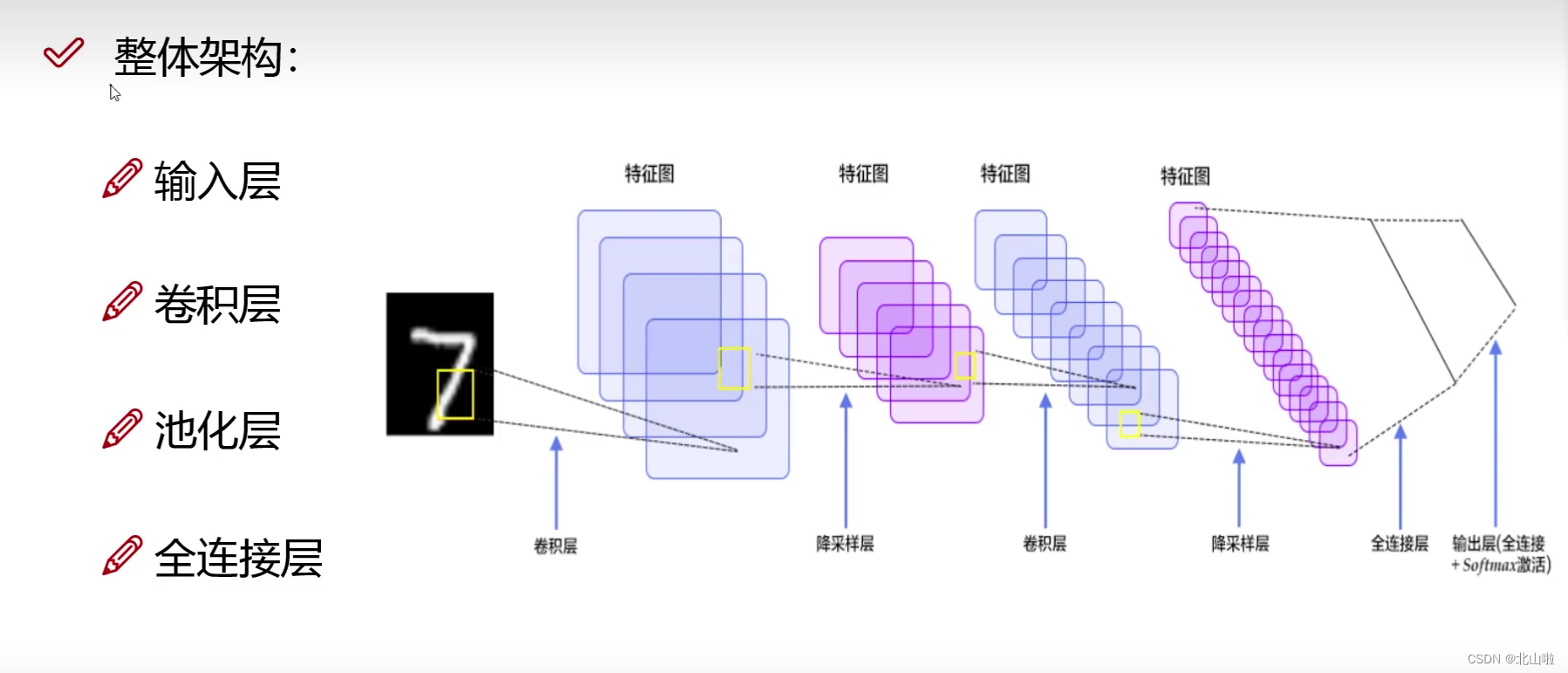
卷积神经网络(CNN)由输入层、卷积层、激活函数、池化层以及全连接层构成。

INPUT（输入层）-CONV（卷积层）-RELU（激活函数）-POOL（池化层）-FC（全连接层）

简单来说：卷积用来提取特征，池化压缩特征，全连接层用来加权重

卷积层

卷积层的作用是用来提取特征，卷积层主要涉及的参数包括：滑动窗口步长，卷积核尺寸，填充边缘，卷积核个数。卷积核的工作原理如下图所示：

如下图所示：输入图像是32 * 32 * 3，3是它的深度也就是R、G、B三通道，通过卷积核，在图中卷积核是5 * 5 * 3的filter,其中filter的深度必须和输入图像的深度相同，也就是对应的3，filter可以有很多个。通过一个filter与输入图像的卷积的话，会得到一个28 * 28 * 1的特征图。

特得到的具体的特征图尺寸的计算公式如下：

如上上图中所示：输入的是32 * 32 * 3大小的图像，用10个5 * 5 *3 的fliter进行卷积操作，并指定步长为1，边缘填充为2：

​ $$(32-5+2\ast 2)/1+1=32$$

输出的规模为32 * 32 * 10，经过卷积操作后也可以保持特征图的长度和宽度不变

关于卷积的过程图解析如下：

输入图像和filter的对应位置元素相乘再求和，最后再加上 b0(偏置),得到特征图。

如图所示：filter w0的第一层深度和输入图像的蓝色方框中对应元素相乘再求和得到0，其他两个深度得到2，0，则有0+2+0+1=3即图中右边特征图的第一个元素3，卷积过后输入图像的蓝色方框再滑动，stride（步长）=2。完成卷积，得到一个3 * 3 * 1的特征图；

边缘填充：在这里还要注意一点，即zero pad项，即为图像加上一个边界，边界元素均为0，这就叫做边缘填充，是为了更好的提取边界的每个部分的特征，让边界点也可以多次的提取特征，这就是padding的作用。

通常，我们会通过多次的卷积，来提取特征。

卷积参数共享：

通过卷积操作，我们实现了输入图像的局部连接，从而大大减少了网络模型中的参数量。但这还不够，利用图像的另一特性，参数量可以进一步降低。

如图所示:10个shape(5,5)的卷积核,每个卷积核在原图中对应一个参数矩阵,大小为5*5。

1. 如果不共享权值的话,将得到$5\ast 5\ast 3\ast 32\ast 32\ast 10+10$ 个参数

2. 如果共享参数的话将有$5\ast 5\ast 3\ast 10+10$ 个参数

总结如下：

卷积层涉及参数

1. 滑动窗口步长：能移动越多得到的特征图越大，提取的特征越细腻，常见步长为1
2. 卷积核尺寸:选择区域的大小—最后得到结果个数的大小，一般3×3
3. 边缘填充:由于步长选择，有些元素重复加权贡献的，越往里的点贡献多，越往外的点贡献少，是边界点贡献多些，在外面加上一圈0，可以弥补一些边界特征缺失）zero padding 以0为值进行边缘填充
4. 卷积核个数：最后要得到多少个特征图,注意的是每个卷积核都是不一样的
5. 卷积参数共享：用同样一组卷积和对图像中每一个区域进行特征提取

池化层

池化层是当前卷积神经网络中常用组件之一，它最早见于LeNet一文，称之为Subsampleor’downsample’即降采样。

池化层是模仿人的视觉系统对数据进行降维，用更高层次的特征表示图像。

池化层的常见操作包含以下几种：最大值池化，均值池化，随机池化，中值池化，组合池化等。

池化层压缩过程：在通过卷积层后对特征图进行筛选，滑动窗口(例如：max pooling将该区域最大值提取出来)，max pooling过程如下：

激活函数

激活函数的作用在于提供网络的非线性建模能力。如果不用激励函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合，这种情况就是最原始的感知机。
  如果使用的话，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

常见的激活函数有：

• Sigmoid激活函数

  也称为S型生长曲线，由于其单增以及反函数单增等性质，Sigmoid函数常被用作神经网络的阈值函数，将变量映射到0,1之间 。公式如下：

  $$f(x)=\frac{1}{1+e^{-x}}$$

  

• Tanh激活函数

  Tanh 激活函数又叫作双曲正切激活函数,在数学中，双曲正切"Tanh"是由基本双曲函数双曲正弦和双曲余弦推导而来。公式如下：

$$f(x)=\frac{e^z-e^{-z}}{e^z+e^{-z}}$$

优点：比Sigmoid函数收敛速度更快,输出以0为中心。
缺点：由于饱和性产生的梯度消失

在实践中，Tanh 函数的使用优先性高于 Sigmoid 函数。负数输入被当作负值，零输入值的映射接近零，正数输入被当作正值。

为了解决梯度消失问题，我们来讨论另一个非线性激活函数-Relu函数，该函数明显优于前面两个函数，是现在使用最广泛的函数。

• Relu激活函数

  公式如下：

  $$Relu=max(0,x)$$
  

当输入 x<0 时，输出为 0，当 x> 0 时，输出为 x。该激活函数使网络更快速地收敛。它不会饱和，即它可以对抗梯度消失问题，至少在正区域（x> 0 时）可以这样，因此神经元至少在一半区域中不会把所有零进行反向传播。由于使用了简单的阈值化（thresholding），ReLU 计算效率很高。

全连接层

全连接层之前的操作：卷积层、池化层、激活函数等的作用是用来提取特征(将原始数据映射到隐藏层特征空间)，而全连接层的作用就是分类(将学到的特征表示映射到样本标记空间当中)

在 CNN 结构中，经多个卷积层和池化层后，连接着1个或1个以上的全连接层．与 MLP 类似，全连接层中的每个神经元与其前一层的所有神经元进行全连接．全连接层可以整合卷积层或者池化层中具有类别区分性的局部信息．为了提升 CNN 网络性能，全连接层每个神经元的激活函数(按你的任务目的选择，分类or回归)。

参考：https://blog.csdn.net/weixin_45829462/article/details/106548749

https://www.zhihu.com/question/41037974/answer/150552142

假设你是一只小蚂蚁，你的任务是找小面包。你的视野还比较窄，只能看到很小一片区域。当你找到一片小面包之后，你不知道你找到的是不是全部的小面包，所以你们全部的蚂蚁开了个会，把所有的小面包都拿出来分享了。全连接层就是这个蚂蚁大会~

如果提前告诉你全世界就只有一块小面包，你找到之后也就掌握了全部的信息，这种情况下也就没必要引入FC层了